Bài giảng Hình học Lớp 10 - Bài 3: Hệ thức lượng trong tam giác (Tiết 1)

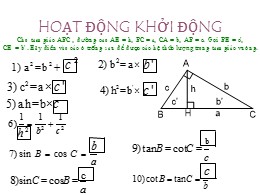
HOẠT ĐỘNG KHỞI ĐỘNG Cho tam gi¸c ABC , ®ư­êng cao AH = h, BC = a, CA = b, AB = c. Gäi BH = c', CH = b' .H·y ®iỊn vµo c¸c « trèng sau ®Ĩ ®­ ư ỵc c¸c hƯ thøc l­ượng trong tam gi¸c vu«ng. 
c 
 b 
HỆ THỨC LƯỢNG TRONG TAM GIÁC 
HỆ THỨC LƯỢNG TRONG TAM GIÁC 
HE ÄTHỨC LƯỢNG TRONG TAM GIÁC VUÔNG 
b 
c 
a 
b’ 
c’ 
h 
H Ệ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG 
Ta biết rằng một tam giác hoàn toàn xác định nếu biết : 
Ba cạnh, 
Hoặc hai cạnh và góc xen giữa, 
Hoặc một cạnh và hai góc kề 
Nghĩa là các yếu tố còn lại của tam giác xác định được 
Để xác định các yếu tố còn lại ta sử dụng các hệ thức liên hệ 
Đó chính là các hệ thức lượng trong tam giác 
Bài toán thực tế 
Đi thẳng theo hai hướng tạo với nhau một góc 60 độ 
Tàu B chạy với vận tốc 15 hải lý một giờ 
Tàu C chạy với vận tốc 20 hải lý môït giờ 
Sau một giờ ,hai tàu cách nhau bao nhiêu hải lí? 
Hai chiếc tàu thuỷ cùng xuất phát từ một vị trí A 
30 
40 
B 
C 
A 
C 
30 
40 
B 
C 
30 
40 
B 
C 
Bài toán hoá 
30 
40 
A 
B 
C 
Cho tam giác ABC 
AB=30, AC=40, 
A=60 độ 
Tính cạnh BC? 
GIẢI 
 § 3. C¸c hƯ thøc lư­ỵng trong tam gi¸c 
BC 
= 
AC - AB 
  
BC 2 
= 
(AC – AB) 2 
 = 
AC 2 + AB 2 – 2AC.AB 
= AC 2 + AB 2 - 
AB 
2AC. 
cosA 
VËy: a 2 = b 2 + c 2 – 2bc cosA 
A 
a 
B 
C 
b? 
c 
Bài toán hoá 
30 
40 
A 
B 
C 
Cho tam giác ABC 
AB=30, AC=40, 
A=60 độ 
Tính cạnh BC? 
GIẢI 
I. §Þnh lÝ cosin:1. Bµi to¸n 2. §Þnh lÝ cosin 
Bµi 3: C¸c hƯ thøc l­ỵng trong tam gi¸c 
 Trong tam gi¸c ABC bÊt k× 
 víi BC = a, CA =b, AB =c ta cã: 
cosA= 
cosB= 
cosC= 
H·y ph¸t biĨu ®Þnh lÝ c«sin b»ng lêi? 
H·y tÝnh cosA, cosB, cosC theo c¸c c¹nh a, b, c? 
Hệ quả: 
Trong một tam giác, bình phương một cạnh bằng tổng b×nh ph­¬ng cđa hai cạnh kia trừ đi hai lần tích của chĩng v µ côsin của g ãc xen gi÷a hai c¹nh ®ã. 
 a 2 = b 2 + c 2 – 2bccosA 
 b 2 + c 2 > a 2 
 b 2 + c 2 = a 2 
b 2 + c 2 < a 2 
cosA > 0 
cosA < 0 
cosA = 0 
A < 90 0 
A = 90 0 
A > 90 0 
*)Mét øng dơng cđa ®Þnh lÝ cosin 
NxÐt :*)Tõ ®.lÝ cosin ta cã thĨ nhËn biÕt mét tam gi¸c lµ vu«ng, nhän hay tï 
 *)§Þnh lÝ Pitago lµ mét tr­ưêng hỵp riªng cđa ®Þnh lÝ Cosin 
 Bµi 3: C¸c hƯ thøc l­ỵng trong tam gi¸c  I. §Þnh lÝ cosin:  1 . §Þnh lÝ cosin  
2. Hệ quả: 
cosA= 
cosB= 
cosC= 
Gọi AM là trung tuyến tam gi¸c ABC. TÝnh AM theo c¸c c¹nh a , b, c 
3. §é dµi trung tuyÕn tam gi¸c 
Cho tam gi¸c ABC cã c¸c c¹nh BC = a, CA = b, AB = c.Gäi m a , m b , m c lµ ®é dµi c¸c ®ư­êng trung tuyÕn lÇn lư­ỵt vÏ tõ c¸c ®Ønh A, B, vµ C cđa tam gi¸c. 
A 
B 
C 
M 
b 
c 
3) VÝ dơ ¸p dơng 
VD1: 
Cho  ABC có các cạnh b = 8 cm, c = 5 cm, 
v à A = 60 0 
a) Tính cạnh a của  ABC. 
b) Tính góc nhỏ nhất của  ABC 
c) Tính độ dài đường trung tuyến của  ABC 
Bài giải 
a)Theo định l Ý cosin ta có 
b) Ta cã: c < a < b nªn < < vËy gãc lµ nhá nhÊt 
Theo hƯ qu¶ cđa ®Þnh lý cosin ta cã: 
c) Aùp dụng công thức 
4) VÝ dơ ¸p dơng 
VD1: 
Cho  ABC có các cạnh b = 8 cm, c = 5 cm, 
v à A=60 0 
a) Tính cạnh a của  ABC. 
b) Tính góc nhỏ nhất của  ABC 
c) Tính độ dài đường trung tuyến của  ABC 
Bài giải 
Bµi 3: C¸c hƯ thøc l­ỵng trong tam gi¸c 
I. §Þnh lÝ cosin:1. Bµi to¸n 2. §Þnh lÝ cosin 
HƯ qu¶: 
3. §é dµi trung tuyÕn tam gi¸c 
VD2: Chøng minh r»ng trong mäi tam gi¸c ABC ta ®Ịu cã:a = b.cosC + c.cosB 
Ta cã VP = b . +c. 
Bµi gi¶i 
4) VÝ dơ ¸p dơng 
= = a = VT 
Hệ quả: 
3. §é dµi trung tuyÕn tam gi¸c 
I. §Þnh lÝ cosin 
1. Bµi to¸n 
Bµi 3: C¸c hƯ thøc l­Ưỵng trong tam gi¸c 
2. §Þnh lÝ cosin 
4) VÝ dơ ¸p dơng 
 cho trư­íc cïng t¸c dơng lªn 1 vËt vµ t¹o thµnh gãc nhän 
Hai lùc 
vµ 
VÝ dơ 3: 
 H·y lËp c«ng thøc tÝnh c­ưêng ®é cđa hỵp lùc 
Theo ®Þnh lÝ cosin ®èi víi tam gi¸c ABC ta cã: 
AC 2 = AB 2 + BC 2 - 2AB.BC.cosB 
hay 
VËy 
A 
B 
C 
D 
Hệ quả: 
3. §é dµi trung tuyÕn tam gi¸c 
I. §Þnh lÝ cosin 
1. Bµi to¸n 
Cđng cè 
2. §Þnh lÝ cosin 
Bµi tËp vỊ nhµ 
Häc thuéc c¸c c«ng thøc 
Lµm bµi tËp tõ 1 ®Õn 7 trang 59 
1. Định lý Cosin trong tam giác 
a/ Chứng minh định lý Pitago 
A 
B 
C 
HD: 
HD: 
Vậy cho tam giác ABC , biết cạnh AB và AC , góc A vuông .Ta sẽ tìm được cạnh BC 
Góc A không vuông? 
b/ Bài toán 
GT: AB,AC,góc A 
KL: BC??? 
A 
B 
C 
Làm sao đây?!?! 
Aùp dụng tương tự bài trên 
HD: 
HD: 
ĐỊNH LÝ 
Trong tam giac ABC ,với BC= a,CA =b , AB =c ta cĩ: 
HỆ QUẢ 
Aùp dụng định lí Cosin trong tam giác ABC, ta có : 
Vậy sau hai giờ hai tàu cáh nhau khoảng 36 hải lí 
Vui h ọchọc vui 
Cho tam giác ABC,AB = c , AC = b , BC = a 
Góc A nhọn, tù, hay vuông? Nếu: 
Chứng minh định lý Pitago 
Ta có 
Do góc A vuông nên : 
Vậy : 
Điều phải chứng minh : 
Ta có : 
Tích vô hướng : 
Do đó : 
Nên: 
Vậy ta tính được cạnh BC 
Buổi học kết thúc 
Các em về nhà nhớ học định lí và làm bài tập đầy đủ