Các dạng lượng giác

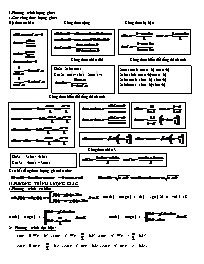
I.Phương trình lượng giác:
1.Các công thức lượng giác:
Hệ thức cơ bản Công thức cộng Công thức hạ bậc
2cosacosb=cos(a+b)+cos(a-b)
2sinasinb=coa(a-b)-cos(a+b)
2sinacosb=sin(a+b)+sin(a-b)
2sinbcosa=sin(a+b)-sin(a-b)
Sin2a=2sinacosa
Cos2a=cos2a– sin2a= 2cos2a–1
	Công thức nhân đôi Công thức biến đổi tổng thành tích
 Công thức biến đổi tổng thành tích	
Công thức nhân 3
Sin3x = 3sinx - 4sin3x 
Cos3x = 4cos3x – 3cosx
Các bất đẳng thức lượng giác cần nhớ:
II.PHƯƠNG TRÌNH LƯỢNG GIÁC
1.Phương trình cơ bản:
 cosf(x) = cosg(x) ó f(x) = ±g(x)+2kp với k ÎZ
tanf(x) =tang(x) ó cotf(x) = cotg(x) ó
2/ Phương trình đặt biệt:
 sinx = 0 Û x = kp , sinx = 1 Û x = + k2p ,sinx = -1 Û x = - + k2p 
 cosx = 0 Û x = + k p , cosx = 1 Û x = k2p , cosx = -1 Û x = p + k2p .
 3/ Phương trình bậc bậc 2 chỉ chứa một hàm số lượng giác :
 Định nghĩa: Là phương trình có dạng trong đó t là một trong bốn hàm số lượng giác: 
 Cách giải:
Bước 1: Đặt t bằng hàm số lượng giác có trong phương trình;
Bước 2: Đặt điều kiện với ẩn phụ t ( t = sinx, t = cosx 1)
Bước 3: Giải phương trình tìm t (thoả mãn điều kiện);
Bước 4: Với mỗi t thoả mãn ta có phương trình lượng giác cơ bản Þ nghiệm x
 4/ Phương trình bậc nhất đối với sinx và cosx . 
Là phương trình có dạng : acosx + bsinx = c (1) trong đó a2 + b2 ¹ 0 
Điều kiện phương trình có nghiệm : 
 Cách giải
Bước 1: Chia 2 vế cho 
Bước 2:
Bước 3: Giải phương trình 
5)Phương trình đẳng cấp đối với sinx và cosx :
 Dạng :asin2x +b sinx cosx + c cos2x = d . (1)
 Cách giải 1:
	Bước 1:
	Xét cosx = 0 => x= => sin2x = 1 (1)=>a=d 
	Nếu đẳng thức đúng =>x = là một nghiệm của pt
	Bước 2:
Xét cosx ≠ 0 : Chia 2 vế cho cosx ,đặt t= tanx
(1)=>at2 + bt +c= d(1+t2)ó (a– d)t2+bt +c – d = 0
Giải phương trình tìm t từ đó suy ra x.
 Cách giải 2:
 Thay 
 Giải pt tìm được suy ra x .
.6)Phương trình đối xứng đối với sinx và cosx :
Dạng a(sinx+cosx) + bsinxcosx + c= 0
Cách giải :
Đặt t = sinx +cosx => sinxcosx =
Pt=> Giải phương trình tìm t
Giải phương trình sinx+cosx=t tìm x
Chú ý : Pt a(sinx–cosx) +bsinxcosx + c = 0 (Đặt t = sinx – cosx )
7)Phương trình lượng giác không mẫu mực
Phương pháp 
–Dùng các phép biến đổi lượng giác thích hợp đưa pt về các dạng phương trình quen biết
–Dùng các phép biến đổi lượng giác và đại số để đưa pt về phương tích có vế phải bằng 0 và các thừa số là những phương trình lượng giác quen biết.
–Đặt ẩn số phụ : Đạt ẩn số phụ thích hợp chuyển về pt đại số :
Một vài nguyên tắc đặt ẩn số phụ:
Nếu phương trình không thay đổi khi ta thay:
x bởi – x đặt ẩn phụ là cosx	b) x bởi p – x đặt ẩn phụ là sinx
 x bởi p + x đặt ẩn phụ là tanx	d) Nếu cả a , b , c đều thõa đặt ẩn phụ là cos2x
e) 	Nếu cả a , ,c đều không thõa chọn ẩn phụ là t = tan
Bài 1: Giải phương trình sau: (1)
ĐK: 
 Bài 2:Giải phương trình : (1)
Bài 3:Giải phương trình cosx+cos2x+cos3x+cos4x+cos5x +cos6x = 0
Bài 4:Giải phương trình sinxcosx+ |sin-cosx|= 
Giải : Đặt t = |sinx-cosx| =>0 £ t £ 
=>t2 =1 –2sinxcosx=>sinxcosx=
Bài 5: Giải phương trình 6sinx– 2cos3x = 5sin2xcosx
Giải :
Nếu cosx = 0 =>sinx = ±1 (1)=>±6=0 (vô lý )=>cosx ≠ 0
Chia 2 vế của phương trình (1) cho cos3x 
Bài 6:Giải phương trình sin8x + cos8x = sin6x+cos6x (1)
Giải
Sin8x +cos8x = (sin4x+cos4x)2–2sin4xcos4x =
 =1- 4 sin2xcos2x +2 sin4xcos4x=1-sin22x+
Sin6x +cos6x =1 – 3sin2xcos2x =1 – 
Bài 7: Giải phương trình cos3x + (1)
GIẢI :
Bài 8:Giải phương trình 
GIẢI:
Bài 9:Giải phương trình sin24x–cos26x=sin (1)
GIẢI : 
Bài 10: Cho phương trình cos3x – 4cos2x + 3cosx – 4 = 0 . Tìm tất cả nghiệm x Î (0; 14 ) của phương trình
GIẢI :
Đặt t = cosx | t | £ 1 (1)=>4t3 – 3t – 4(2t2 –1 ) + 3t –4 = 0 ó 4t3 –8t2 =0 ó
t= 0 \=>cosx= 0=> x= 
Do x Î(0;14)=> 0 < 
BÀI TẬP
1.Giải các phương trình sau:
HỆ THỨC LƯỢNG TRONG TAM GIÁC
I,CÁC CÔNG THỨC CẦN NHỚ:
Các công thức tính diện tích tam giác
Định lý hàm số cosin
a2=b2 +c2 –2bc cosA b2 = c2+a2 –2cacosB
c2= a2+c2 –2abcosC
Định lý hàm số sin
Định lý về đường trung tuyến
Bài 1:Cho tam giác ABC có diện tích S và R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh :
Sin2A+sin2B+sin2C= 
Giải : 
VT= sin2A+sin2B+sin2C= 2sin(A+B)cos(A-B)+2sinCcosC=2sinC[cos(A–B)–cos(A+B)]=4sinAsinBsinC
 =4
Bài 2:Cho tam giác ABC có 3 góc A ; B ; C theo thứ tự tạo thành một cấp số nhân công bội 2 . 
a)Chứng minh 
b)Tính A=cos2A +cos2B +cos2C = 5/4 với a ; b ; c là độ dài 3 cạnh BC ;CA ; và AB của tam giác ABC
Giải
Theo định lý hàm số sin a = 2Rsin b = 2Rsin c = 2Rsin
Bài 3:Xác định hình dang của tam giác ABC biết các cạnh và các góc của nó thõa: 
GIẢI:
A;B ≠ 
 Bài 4:Cho tam giác ABC có các cạnh a;b ;c và các góc A ;B ;C thõa : Chứng minh tam giác ABC đều,
GIẢI:
Bài 5:Cho tam giác ABC có 3 góc A ; B ; C tạo thành một cấp số công và A £ B £ C và thõa hệ thức , cho biết bán kính đường tròn nội tiếp r = 1.Tính số đo 3 góc và độ dài 3 cạnh của tam giác ABC.
GIẢI:
A ; B ; C là cấp số cộng =>A+C=2B mà A+B+C=1800 =>B=600 =>A+C=1200
Bài 6:Cho tam cân có cạnh đáy là a cạnh bên b góc ở đỉnh là 200 . chứng minh a3 +b3 =3ab2
Giải:
Gọi H là trung điểm của BC=>ÐBAH=100
BÀI TẬP
1)Xác định hình dạng của tam giác ABC biết
a)sin4A+sin4B+sin4C = 0 (Tam giác ABC vuông )	b) (Tam giác cân)
c)	d) (Tam giác đều)
2)Trực tâm H của tam giác ABC cách đỉnh A bằng đường cao AA’. Chứng minh các đẳng thức sau:
a)tanB.tanC= 3 b)2tanA=tanB+tanC	c)cos(B – C) = 2cosA
3.Cho tam giác ABC . Chứng minh rằng A = 2B óa2 = b2 +bc
4.Chứng minh rằng nếu O là tâm của đường tròn nội tiếp tam giác ABC thì OA.OB.OC =4Rr2 
5.Cho tam giác ABC có 3 góc A ; B ;C tạo thành cấp số nhân có công bội q = 2.Tính a2+b2+c2 (ĐS:7)