Các dạng toán liên quan đến khảo sát hàm số

CÁC DẠNG TOÁN LIÊN QUAN ĐẾN KHẢO SÁT HÀM SỐ
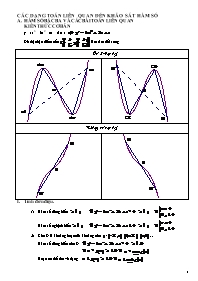
A.	HÀM SỐ BẬC BA VÀ CÁC BÀI TOÁN LIÊN QUAN
KIẾN THỨC CƠ BẢN
y = ax3 + bx2 + cx + d (a ¹ 0)
Đồ thị nhận điểm uốn làm tâm đối xứng
	Coù 2 cöïc trò
Khoâng coù cöïc trò
I.	Tính đơn điệu.
Hàm số đồng biến 	Hàm số nghịch biến	
Cho D là khoảng hoặc nửa khoảng trên :, , . . .	Hàm số đồng biến trên D	Hoặc có thể đưa về dạng	
II.	Cực trị.
Tính nhanh cực trị: 	
	Chia y cho y’ ta được: 
	Nếu là điểm cực trị thì 
	Phương trình đường thẳng qua hai điểm cực trị là 
Hàm số bậc ba không có cực trị, hoặc có hai cực trị.
	Hàm số không có cực trị 	
Hàm số có cực trị (có hai cực trị)	
Hàm số có cực trị sao cho hoành độ của cực đạt nhỏ hơn hoành độ của cực tiểu	Hàm số có cực trị sao cho hoành độ của cực đạt lớn hơn hoành độ của cực tiểu
	Hàm số đạt cực trị tại 	Hàm số đạt cực đạt tại 	
	Hàm số đạt cực tiểu tại 
Hàm số đạt cực trị tại , sao cho
	a)	(cực trị có hoành độ âm),	 (cực trị có hoành độ dương)
b)	 (hoành độ của 2 cực trị trái dấu, 2 điểm cực trị nằm về hai phía của trục oy)
c)	, 	, 	
	d)	, thỏa biểu thức nào đó ( sử dụng Viet: , )
Trung điểm của hai cực trị thuộc trục Ox
	Khoảng cách từ hai điểm cực trị đến trục ox là bằng nhau
	 Điểm đối xứng của đồ thị thuộc Ox	Điểm uốn thuộc trục Ox
	Hướng dẫn:
	Để hàm số có hai cực trị thì y’ = 0 có hai nghiệm phân biệt
Trung điểm của hai cực trị , điểm này thuộc Ox khi 
Có hai cực trị đối xứng nhau qua ( hai cực trị cách đều điểm I )	là trung điểm của hai cực trị 	Hướng dẫn:
	Để hàm số có hai cực trị thì y’ = 0 có hai nghiệm phân biệt 
là trung điểm của hai cực trị khi: và 
x1
x2
y(x2)
y(x1)
O
Hàm số có hai điểm cực trị nằm về hai phía của trục Ox	Hướng dẫn:
Hàm số có hai cực trị khi 
	Để hai điểm cực trị nằm về hai phía của trục Ox thì 
	Trong đó , là nghiệm của phương trình 
tức là , 
	Chú ý:	
x1
x2
y(x2)
y(x1)
O
x1
x2
y(x2)
y(x1)
O
Hàm số có hai điểm cực trị nằm về một phía của trục Ox	
x1
x2
y(x2)
y(x1)
O
Hàm số có hai điểm cực trị nằm phía trên của trục Ox	
x1
x2
y(x2)
y(x1)
O
Hàm số có hai điểm cực trị nằm phía trên của trục Ox	
III.	Sự tương giao.
	1)	Đồ thị hàm số cắt Ox tại 3 điểm phân biệt (tức phương trình y = 0 có 3 nghiệm pb)
 Hàm số có hai điểm cực trị nằm về hai phía của trục Ox
Chú ý: 
Nếu ( nhẩm nghiệm)
Thì phương trình y = 0 có 3 nghiệm pb có 2 nghiệm pbiệt khác 
	2)	(C) cắt Ox tại 3 điểm phân biệt cách đều nhau 
Û Trung điểm của hai cực trị thuộc trục Ox
Û y’ = 0 có 2 nghiệm phân biệt và 
3)	Đồ thị hàm số cắt Ox tại một điểm
 Hàm số có hai điểm cực trị nằm về một phía của trục Ox hoặc không có cực trị
	hoặc 
Chú ý: 
Nếu ( nhẩm nghiệm)
Thì pt y = 0 có 1 nghiệm vô nghiệm hoặc có nghiệm kép bằng 
	4)	Đường thẳng d qua có hệ số góc k cắt tại 3 điểm phân biệt
	Hướng dẫn:
	Đường thẳng d có phương trình 
	Xét phương trình 
	Để (C) cắt d tại 3 điểm phân biệt thì phương trình có 2 nghiệm phân biệt khác 
BÀI TẬP
Tính đơn điệu.
1) 	Tìm m để các hàm số sau đồng biến trên tập xác định.
y = x3 -3mx2 + (m + 2)x – 1 	ĐS: 
2) 	Tìm m để các hàm số sau nghịch biến trên tập xác định.
y = 	ĐS: m
3)	Tìm m để các hàm số:
y = , nghịch biến trên khoảng (1 ; 	ĐS: m
y = x3 + 3x2 + (m – 1)x + 4m, nghịch biến trên khoảng (-1 ; 1) 	ĐS: m
Cực trị.
1)	Xác định m để hàm số có CĐ và CT : y = x3 + mx2 + 3mx + 5
	Đáp số: m 9
2)	[ĐHBK_2000]. Tìm m để hàm số không có cực trị y = mx3 + 3mx2 – (m - 1)x – 1	
Đáp số: 0 £ m £ 1/4 
3)	[ĐH Huế D_97]. Cho hàm số y = -(m2 + 5m)x3 + 6mx2 + 6x – 6 
Với giá trị nào của m thì hàm số đạt CĐ tại x = 1	
Đáp số: m = 1
4)	Cao Đẳng 2009 Khối A, B, D. 
Cho hàm số 	(1)
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = 2
2. Tìm các giá trị của m để hàm số (1) có cực đại, cực tiểu và các điểm cực trị của hàm số (1) có hoành độ dương.
5)	Tìm m để hàm số đạt cực trị tại thỏa mãn điều kiện 
Đáp số:
6)	[ĐHQG TPHCM A_01]. Cho hàm số y = 2x3 + 3(m - 3)x2 + 11 – 3m 
Tìm m để đồ thị hàm số có CĐ và CT. Lập PT đường thẳng đi qua CĐ và CT 
	Đáp số: m ¹ 3, y = -(m - 3)2x + 11 – 3m
7) 	Tìm m để hàm số có đường thẳng đi qua cực đại và cực tiểu vuông góc với đường thẳng 
Đáp số:
8)	Cho hàm số y = mx3 – 3mx2 + (2m + 1)x + 3 – m. 
Xác định m để hàm số có CĐ và CT. 
CMR khi đó đường thẳng nối CĐ, CT luôn đi qua một điểm cố định
	Đáp số: m 1; y = (m - 1)x + (10 - m), điểm cố định A(-1/2; 3) 
9)	[Đại học Đà Nẵng, 2000]. Cho hàm số . Xác định m để đồ thị của hàm số có hai điểm cực đại và cực tiểu nằm về hai phía của trục tung.
Đáp số:
10)	[Đại học Quốc gia Hà Nội, 1997]. Cho hàm số (a là tham số). Với những giá trị nào của a thì đồ thị của hàm số có điểm cực đại, điểm cực tiểu, các điểm này cách đều trục tung.
Đáp số: .
11)	Cho hàm số . Định m để hàm số có cực đại và cực tiểu đồng thời hai giá trị cực trị cùng dấu. 
Đáp số:.
12)	Cho hàm số y = 4x3 – mx2 – 3x + m. 
CMR " m hàm số luôn có CĐ, CT đồng thời hoành độ các điểm CĐ, CT luôn trái dấu	
Đáp số: xCĐ.xCT = -1/4 < 0
13)	Đại Học 2007 Khối B 
	Cho hàm số 	(1)
1. 	Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = 1
2. 	Tìm các giá trị của m để hàm số (1) có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số (1) cách đều góc tọa độ O.
14) 	Cho hàm số y = 2x3 + 3(m - 1)x2 + 6(m - 2)x – 1. 
Tìm m để hàm số đạt CĐ, CT tại x1, x2 và 	
Đáp số: m = -1
15)	[HVQHQT Khối D năm 2001].Cho ham số . 
Tìm m để hàm số có khoảng cách giửa hai điểm cực trị là nhỏ nhất.
Đáp số:m = 0
16)	[ĐH Huế A_01] Xác định m để hàm số y = x3- mx2 + m3 có các điểm CĐ, CT đối xứng nhau qua đường thẳng y = x	
Đáp số: m ¹ 0 (có CĐ, CT), m = ± .
Sự tương giao
1)	Cho hàm số 
	Tìm m để đồ thị hàm số cắt Ox tại 3 điểm phân biệt có hoành độ lớn hơn 1
	Đáp số:
2)	[ĐHKT 98]. Cho hàm số , đường thẳng d qua và có hệ số góc bằng k
	Xác định k để đường thẳng d cắt đồ thị tại 3 điểm phân biệt
Đáp số:
3)	Đại Học 2006 Khối D
Cho hàm số 	
1. Khảo sát sự biến thiên và vẽ đồ thị (C) hàm số đã cho.
2. Gọi d là đường thẳng qua điểm và có hệ số góc là m, tìm m để đường thẳng d cắt đồ thị (C) tại 3 điểm phân biệt.
	Đáp số:
4)	Đại Học 2008 Khối D
Cho hàm số 	(1)
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số (1)
2. Chứng minh rằng mọi đường thẳng đi qua điểm với hệ số góc k () đều cắt đồ thị hàm số (1) tại ba điểm phân biệt I, A, B đồng thời I là trung điểm của đoạn thẳng AB.
B.	HÀM SỐ BẬC 4 VÀ CÁC BÀI TOÁN LIÊN QUAN.
KIẾN THỨC CƠ BẢN
Đồ thị nhận trục Oy làm trục đối xứng
Coù 3 cöïc trò
Coù 1 cöïc trò
I.	Cực trị.
	, 	
	1)	Tính nhanh cực trị và parabol qua ba điểm cực trị
	Chia y cho y’ ta được:
	Nếu là điểm cực trị thì 
	Vậy đường cong qua các điểm cực trị là parabol 
	2)	Hàm số có 1 cực trị hoặc có 3 cực trị
® Hàm số có một cực trị	
	® Hàm số có ba cực trị	
	3)	Hàm số có cực tiểu không có cực đại 
	Đồ thị là parabol quay lên 
	4)	Hàm số có cực đại không có cực tiểu 
	Đồ thị là parabol quay xuống 
	5)	Hàm số có hai cực tiểu, một cực đại	 
6)	Hàm số có hai cực đại, một cực tiểu	 
II.	Sư tương giao.
	Số giao điểm của đồ thị và trục Ox là số nghiệm của phương trình 	(1)
	Đặt , khi đó phương trình (1) tương đương: 	(2)
	Ta thấy mổi nghiệm của phương trình (2) cho ta hai nghiệm của phương trình (1)
Đồ thị cắt Ox tại 4 điểm phân biệt	(1)	có 4 nghiệm phân biệt	(2)	có 2 nghiệm dương phân biệt
Đồ thị cắt Ox tại 2 điểm	(1)	có 2 nghiệm	(2)	có 1 nghiệm dương	
Đồ thị cắt Ox tại 3 điểm	(1)	có 3 nghiệm	(2)	có 1 nghiệm bằng 0, 1 nghiệm dương	
Đồ thị cắt Ox tại 1 điểm	(1)	có 1 nghiệm	(2)	có 1 nghiệm bằng 0	
Đồ thị không cắt Ox	(1)	không có nghiệm	(2)	vô nghiệm hoặc có hai nghiệm âm	
Đồ thị cắt Ox tại bốn điểm lập thành cấp số cộng	(1) có bốn nghiệm <<< lập thành cấp số cộng (tức , )	(2) có hai nghiệm dương và lập thành cấp số cộng	Từ đó 	Giải hệ phương trình:
BÀI TẬP
Đại học cảnh sát 2000	Tìm m để hàm số chỉ có cực tiểu mà không có cực đại.	Đáp số:	
	Đại học kiến trúc 1999	Tìm k để hàm số chỉ có một điểm cực trị.	Đáp số: hoặc 	
	Đại Học 2002 Khối B	Cho hàm số 	(1)	1.	Khảo sát sự biến thiên của hàm số (1) khi m = 1	2.	Tìm m để hàm số (1) có ba điểm cực trị.
	HVQHQT 1997 	Xác định m để hàm số có cực đại cực tiểu lập thành tam giác đều.	Đáp số:
	Dự bị 2004	Cho hàm số y = x4 - 2m2x2 + 1	1. Khảo sát và vẽ đồ thị với m=1	2. Tìm m để đồ thị hàm số có 3 điểm cực trị là 3 đỉnh của một tam giác vuông cân.	Đáp số:	
	ĐHSP II 1997. 	Cho hàm số y= (1-m) x4-mx3 +2m-1	Tìm m để hàm số có cực đại và cực tiểu mà tổng bình phương các hoành độ bằng 27.	Đáp số:
Sự tương giao
ĐHCĐ dự bị.2002 	Cho hàm số y=x4 –mx2+ m -1	1. Khảo sát và vẽ đồ thị hàm số khi m=8.	2. Tìm m để đồ thị hàm số cắt trục ox tại 4 điểm phân biệt.	Đáp số:	
Cho . Tìm m để cắt Ox tại bốn điểm phân biệt lập thành cấp số cộng.	Đáp số: hoặc 	
Đại Học 2009 Khối D	Cho hàm số y = x4 – (3m + 2)x2 + 3m có đồ thị là (Cm), m là tham số.	1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m = 0.	2. Tìm m để đường thẳng y = -1 cắt đồ thị (Cm) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2.	Đáp số:	
	ĐHQG TPHCM 1996 	Cho Cm : y= x4 -2 m x2 + m3-m2	1. Khảo sát và vẽ đồ thị hàm số ứng với m = 1	2. Tìm m để hàm số tiếp xúc với trục hoành tại 2 điểm phân biệt.	Đáp số:	
ĐH Huế 2000 	1. Khảo sát và vẽ đồ thị của hàm số y= x4-5x2+4	2. Tìm m để đường thẳng y = m cắt đồ thị 3 đoạn thẳng bằng nhau.	Đáp số:
C.	HÀM NHẤT BIẾN VÀ CÁC BÀI TOÁN LIÊN QUAN.
KIẾN THỨC CƠ BẢN
Đồ thị đối xứng qua giao điểm I của hai tiệm cận
I.	Tính đơn điệu.
Hàm số luôn đồng biến hoặc luôn nghịch biến trên từng khoảng xác định nên nên không có cực trị và gọi là hàm nhất biến.
	●	Nếu hàm số đồng biến trên từng khoảng xác định
	●	Nếu hàm số nghịch biến trên từng khoảng xác định
II.	Tiệm cận.
Tiệm cận đứng , tiệm cận ngang 
Tích khoảng cách từ một điểm bất kỳ thuộc đồ thị đến hai tiệm cận là không đổi.
III.	Tích chất của tiếp tuyến.
Nếu M thuộc đồ thị (C), tiếp tuyến tại M cắt hai đường tiệm cận tại A và B thì:	
●	M là trung điểm của AB.
●	Tam giác MAB có diện tích không đổi.
Nếu M thuộc một trong hai đường tiệm cận thì qua M chỉ kẻ được một tiếp tuyến với (C).
IV.	Sự tương giao.
	Giao điểm của đồ thị và đường thẳng 
	Xét phương trình 
	( đều không là nghiệm của 2 phương trình trên)
	(¯)
	●	(C) cắt d tại 2 điểm phân biệt 	 (¯) có hai nghiệm phân biệt.
	●	(C) cắt d tại 1 điểm 	 (¯) có 1 nghiệm.
●	(C) không cắt d 	 (¯) vô nghiệm.
V.	Điểm đặt biệt.
	Hai điểm thuộc hai nhánh sao cho khoảng cách giữa hai điểm đó là ngắn nhất
BÀI TẬP.
Cho hàm số 	a)	Khảo sát và vẽ đồ thị (C)	b)	Chứng minh rằng tích khoảng cách từ một điểm bất kỳ thuộc đồ thị (C) đến hai tiệm cận là 	không đổi.	c)	Chứng minh rằng tiếp tuyến tại điểm M bất kỳ thuộc đồ thị (C) cắt hai đường tiệm cận tại A, 	B thì M là trung điểm của AB và diện tích tam giác MAB không đổi.	d)	N là điểm thuộc tiệm cận đứng, chứng minh rằng qua N chỉ kẻ được một tiếp tuyến với (C).
Cho hàm số 	a)	Khảo sát và vẽ đồ thị (C) của hàm số đã cho.	b)	Chứng minh (C) luôn cắt tại hai điểm A, B xác định m để AB ngắn nhất.	c)	Tìm hai điểm M, N thuộc hai nhánh của (C) sao cho khoảng cách MN ngắn nhất.	d)	Tìm M thuộc (C) để MI ngắn nhất, trong trường hợp này tiếp tuyến của (C) tại M vuông góc 	với MI.	e)	Gọi (D) là đường thẳng có phương trình với . Tìm điểu kiện của b để tồn 	tại a sao cho (D) tiếp xúc với (C).
Cao Đẳng 2008 Khối A, B, D 	Cho hàm số 	1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.	2. Tìm m để đường thẳng cắt đồ thị (C) tại hai điểm phân biệt.
CĐSP TV khối A năm 2005	Cho hàm số	Chứng minh rằng luôn cắt (C) tại hai điểm phân biệt A, B. Tìm m để AB ngắn I.	Đáp số:
CĐSP TPHCM Khối A năm 2004	Cho hàm số 	a)	Xác định m để cắt (C) tại hai điểm phân biệt A, B sao cho tiếp tuyến tại A và 	B song song nhau.	b)	Tìm m thuộc (C) sao cho tổng khoảng cách từ M đến hai tiệm cận là ngắn nhất.	Đáp số: a) , b)
PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ 
I. 	KIẾN THỨC CƠ BẢN.
a) 	Phương trình tiếp tuyến tại M(x0 , y0 )Î(C)	
(D) : y = f ’(x0)(x-x0) + y0
b)	Phương trình tiếp tuyến có hệ số góc k cho trước
	i)	Tiếp tuyến song song với đường thẳng 
o	Phương trình tiếp tuyến có dạng (D): 	y = f ’(x0)(x-x0) + y0
o	Tiếp tuyến (D) song song với đường thẳng khi : f ’(x0) = a
 	Giải phương trình tìm x0 suy ra y0 ? thế vào phương trình D 
	ii)	Tiếp tuyến vuông góc với đường thẳng 
o	Phương trình tiếp tuyến có dạng (D) : 	y = f ’(x0)(x-x0) + y0
o	Tiếp tuyến (D) vuông góc với đường thẳng khi : f ’(x0) a= –1
 	Giải phương trình tìm x0 suy ra y0 ? thế vào phương trình D 
c) 	Phương trình tiếp tuyến qua A (xA,yA) 
o	Phương trình tiếp tuyến có dạng (D) : 	y = f ’(x0)(x-x0) + y0
 	o	Đường thẳng (D) qua A(xA; yA) khi:	yA= f ’(x0)(xA-x0) + f(x0)
 	Giải phương trình tìm x0 suy ra y0 ? thế vào phương trình D 
d)	Điều kiện tiếp xúc của hai đồ thi hàm số và là 
	Từ đó ta có cách viết phương trình tiếp tuyến qua A (xA,yA) như sau:
Cách 2:
	o	Phương trình đường thẳng qua A (xA,yA) có dạng 
	o	D tiếp xúc với (C) khi và chỉ khi hệ sau có nghiệm
	Giải hệ phương trình tìm k ? thế vào phương trình D
	Ví dụ 1.	Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm 
	Đáp số:	
Ví dụ 2.	Viết phương trình tiếp tuyến của đồ thị hàm số , biết tiếp tuyến vuông góc với đường thẳng .	Đáp số:	
	Ví dụ 3.	Viết phương trình tiếp tuyến với đồ thị hsố biết tiếp tuyến qua 
	Đáp số:	, 
BÀI TẬP.
Viết phương trình tiếp tuyến của đồ thị hàm số , biết :	a)	Tiếp điểm có hoành độ x = 3	b)	Tiếp tuyến qua 	c)	Tiếp tuyến song song với đường thẳng 	Đáp số:	a),	b) ,,	c) ;
Cho đồ thị hàm số 	a)	Tìm phương trình đường thẳng d tiếp xúc với đồ thị (C) tại .	b)	Tìm đường thẳng tiếp xúc với (C) và qua .	c)	Tìm đường thẳng vuông góc với và tiếp xúc với (C).	Đáp số:	a)	,	b);;,	c)	
Cho hàm số có đồ thị là (C)	a)	Lập phương trình tiếp tuyến của (C) tại giao điểm của nó với hai trục tọa độ.	b)	Tìm đường thẳng tiếp xúc với (C) và qua 	c)	Tìm đường thẳng song song với và tiếp xúc với đồ thị (C)	Đáp số:	a);, b);,	 c); 	
Đại Học 2008 Khối B	Cho hàm số 	(1)	1. 	Khảo sát sự biến thiên và vẽ đồ thị hàm số (1)	2.	Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết rằng tiếp tuyến đó qua điểm 	Đáp số:, 
Đại Học 2005 Khối D	Gọi là đồ thị hàm số 	(*)	1.	Khảo sát sự biến thiên và vẽ đồ thị hàm số (*) khi m = 2	2.	Gọi M là điểm thuộc có hoành độ bằng – 1. Tìm m để tiếp tuyến của tại điểm M song 	song với đường thẳng 	Đáp số:
Cho hàm số y = 2x3 + 3x2 – 12x – 1. Tìm M Î đồ thị (C) của hàm số đã cho sao cho tiếp tuyến tại M 	đi qua gốc tọa độ O.	Đáp số: 
Chứng minh rằng từ có thể vẽ được hai tiếp tuyến vuông góc nhau đến đồ thị hàm số 	.	
Cho hàm số y = -x4 + 2mx2 – 2m + 1. Tìm m để các tiếp tuyến của đồ thị hàm số tại A(1;0), B(-1;0) 	vuông góc nhau.	Đáp số: ;
Cho hàm số	a)	Chứng minh rằng (C) không có hai điểm nào mà tại đó hai tiếp tuyến vuông góc nhau	b)	Tìm k để đồ thị hàm số có tiếp tuyến vuông góc với đường thẳng 	
Cho hàm số	a)	Tìm m để cắt đường thẳng y = 1 tại ba điểm và B, C.	b)	Tìm m để tiếp tuyến tại B và C vuông góc nhau.	Đáp số: a)	b)
Cho hàm số	(Phạm An Hòa – 339 )	Tìm m để cắt đường thẳng tại ba điểm phân biệt , B , C sao cho tiếp tuyến 	tại B và C vuông góc nhau.	Đáp số: 	
Tìm những điểm trên trục trung mà tại đó có thể kẽ được ba tiếp tuyến với đồ thị hàm số	 	Đáp số: 
Cho hàm số	( TT – LHĐ – 152 )	Chứng minh rằng từ một điểm bất kỳ trên đương thẳng x = 2 chỉ có thể kẻ được 1 tiếp tuyến với (C).
Cho hàm số	( ĐH Nông Lâm 2001) 	Tìm những điểm trên ox mà từ đó kẻ được 3 tiếp tuyến với (C) trong đó có 2 tiếp tuyến vuông góc 	nhau.	Đáp số: 
Cho hàm số( TT – LHĐ – 178 )	Tìm những điểm trên oy mà tại đó chỉ kẻ được một tiếp tuyến với (C)	Đáp số: 	
Cho hàm số( TT – LHĐ – 153 )	Tìm những điểm trên đường thẳng y = 2 mà từ đó kẻ được 3 tiếp tuyến với (C)	Đáp số: với 
Cho hàm số	Tìm m để tiếp tuyến của đồ thị tại giao điểm của đồ thị với trục hoành sẽ song song với đường thẳng 	. Viết phương trình tiếp tuyến đó.	Đáp số: 	, , ;	, , 	
Cho hàm số	Tìm m để nhận đường thẳng làm tiếp tuyến tại điểm có hoành độ x = 1.	
Cho hàm số	(Học Viện Quân Y 1997)	a) 	Viết phương trình tiếp tuyến tại giao điểm của và trục oy.	b)	Tìm m để tiếp tuyến nói trên chắn hai trục tọa độ 1 tam giác có diện tích bằng 8.	Đáp số:	a)	b), 
Đại Học 2007 Khối D	Cho hàm số 	1.	Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.	2.	Tìm tọa độ điểm M thuộc (C), biết tiếp tuyến của (C) tại M cắt Ox, Oy tại A, B và tam giác OAB 	có diện tích bằng 4.
Đại Học 2009 Khối A	Cho hàm số 	(1)	1. 	Khảo sát sự biến thiên và vẽ đồ thị hàm số (1)	2.	Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung tại 	hai điểm phân biệt A, B và tam giác OAB cân tại góc tọa độ O.
Cho hàm số	(Kinh Tế Quốc Dân Hà Nội 1998)	Chứng minh rằng trong tất cả các tiếp tuyến của (C) tiếp tuyến tại điểm uốn có hệ số góc nhỏ nhất.
Đại Học 2004 Khối B	Cho hàm số 	(1)	1. 	Khảo sát sự biến thiên và vẽ đồ thị hàm số (1)	2.	Viết phương trình tiếp tuyến của đồ thị hàm số (1) tại điểm uốn, chứng minh rằng là tiếp 	tuyến của đồ thị hàm số (1) có hệ số góc nhỏ nhất.– ¥
-2
0