Chuyên đề Toán Lớp 10 - Chuyên đề 9: Hệ thức lượng giác trong tam giác
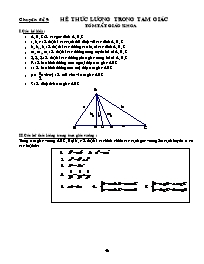
· A, B, C: là các góc đỉnh A, B, C
· a, b, c : là độ dài các cạnh đối diện với các đỉnh A, B, C
· ha, hb, hc : là độ dài các đường cao hạ từ các đỉnh A, B, C
· ma, mb, mc : là độ dài các đường trung tuyến kẻ từ A, B, C
· la, lb, lc : là độ dài các đường phân giác trong kẻ từ A, B, C
· R : là bán kính đường tròn ngoại tiếp tam giác ABC
· r : là bán kính đường tròn nội tiếp tam giác ABC
· p = (a+b+c) : là nữa chu vi tam giác ABC
S : là diện tích tam giác ABC
Bạn đang xem tài liệu "Chuyên đề Toán Lớp 10 - Chuyên đề 9: Hệ thức lượng giác trong tam giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Chuyên đề 9: HỆ THỨC LƯỢNG TRONG TAM GIÁC TÓM TẮT GIÁO KHOA I. Các ký hiệu: A, B, C: là các góc đỉnh A, B, C a, b, c : là độ dài các cạnh đối diện với các đỉnh A, B, C ha, hb, hc : là độ dài các đường cao hạ từ các đỉnh A, B, C ma, mb, mc : là độ dài các đường trung tuyến kẻ từ A, B, C la, lb, lc : là độ dài các đường phân giác trong kẻ từ A, B, C R : là bán kính đường tròn ngoại tiếp tam giác ABC r : là bán kính đường tròn nội tiếp tam giác ABC p = (a+b+c) : là nữa chu vi tam giác ABC S : là diện tích tam giác ABC II. Các hệ thức lượng trong tam giác vuông : Trong tam giác vuông ABC . Gọi b', c' là độ dài các hình chiếu các cạnh góc vuông lên cạnh huyền ta có các hệ thức: II. Các hệ thức lượng trong tam giác thường 1. Định lý hàm số CÔSIN: Trong tam giác ABC ta luôn có : Ghi nhớ: Trong một tam giác, bình phương mỗi cạnh bằng tổng bình phương hai cạnh kia trừ đi hai lần tích hai cạnh ấy với côsin của góc xen giữa chúng. Hệ quả: Trong tam giác ABC ta luôn có : , , 2. Định lý hàm số SIN: Trong tam giác ABC ta có : Hệ quả: Với mọi tam giác ABC, ta có: Ghi nhớ: Trong một tam giác, tỷ số giữa một cạnh của tam giác và sin của góc đối diện với cạnh đó bằng đường kính đường tròn ngoại tiếp tam giác. 3. Định lý về đường trung tuyến: Trong tam giác ABC ta có : 4. Định lý về diện tích tam giác: Diện tích tam giác ABC được tính theo các công thức sau: 5. Định lý về đường phân giác: CÁC DẠNG TOÁN CƠ BẢN Dạng 1: CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC Để chứng minh đẳng thức lượng giác A=B ta có thể thực hiện theo một trong các phương pháp sau Phương pháp 1: Biến đổi vế này thành vế kia Phương pháp 2: Xuất phát từ một một hệ thức đúng đã biết để suy ra đẳng thức cần chứng minh VÍ DỤ MINH HỌA: Ví dụ 1: Cho tam giác ABC. Chứng minh các đẳng thức sau: a) b) Ví dụ 2: Cho tam giác ABC. Chứng minh các đẳng thức sau: a) (ABC không vuông) b) Dạng 2: CHỨNG MINH BẤT ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC I. Bất đẳng thức trong tam giác : Nếu a, b, c là ba cạnh của một tam giác thì : a > 0, b > 0, c > 0 II. Các bất đẳng thức cơ bản : 1. Bất đẳng thức Cauchy: Cho hai số không âm a; b ta có : Dấu "=" xãy ra khi và chỉ khi a=b Tổng quát : Cho n số không âm a1,a2,...an ta có : Dấu "=" xãy ra khi và chỉ khi a1 = a2 =...= an 2 . Bất đẳng thức Bunhiacốpski : Cho bốn số thực a,b,x,y ta có : Dấu "=" xãy ra khi và chỉ khi ay = bx Tổng quát : Cho hai bộ số và ta có : Dấu "=" xãy ra khi và chỉ khi với quy ước rằng nếu mẫu bằng 0 thì tử cũng bằng 3) Bất đẳng thức cơ bản: a) Cho hai số dương x, y ta luôn có: Dấu "=" xãy ra khi và chỉ khi x = y b) Với mọi số thực x, y ta luôn có: Dấu "=" xãy ra khi và chỉ khi x = y III. Bất đẳng thức JENSEN : 1) Nếu hàm số y=f(x) có đạo hàm cấp hai f''(x) < 0 (f là hàm lồi) thì Với mọi ta có: Dấu "=" xãy ra khi và chỉ khi 2) Nếu hàm số y=f(x) có đạo hàm cấp hai f''(x) > 0 (f là hàm lõm) thì Với mọi ta có: Dấu "=" xãy ra khi và chỉ khi Để chứng minh đẳng thức lượng giác AB (>,) ta có thể thực hiện theo một trong các phương pháp sau: Phương pháp 1: Biến đổi bất đẳng thức cần chứng minh đến đến một bất đẳng thức hiển nhiên đúng Phương pháp 2: Sử dụng các bất đẳng thức cơ bản đã biết (Cô si, BCS,...) để suy ra bất đẳng thức cần chứng minh VÍ DỤ MINH HỌA: Ví dụ 1: Cho tam giác ABC. Chứng minh rằng: Ví dụ 2: Cho tam giác ABC. Chứng minh rằng: a) b) c) Ví dụ 3: Cho tam giác ABC. Chứng minh rằng: a) b) c) Dạng 3: NHẬN DẠNG TAM GIÁC KIỂU ĐỀ TOÁN 1: KIỂU ĐỀ TOÁN 2: "Điều kiện cho trước" có thể là: Đẳng thức lượng giác về góc Đẳng thức lượng giác + độ dài (cạnh, trung tuyến, phân giác,...) Đẳng thức độ dài Hệ đẳng thức 1) Nhận dạng tam giác vuông Phương pháp: Sử dụng các phép biến đổi tương đương hoặc hệ quả để biến đổi "Điều kiện cho trước" đến một đẳng thức mà từ đó ta dể dàng kết luận được tính chất của tam giác 2) Nhận dạng tam giác cân Phương pháp: Sử dụng các phép biến đổi tương đương hoặc hệ quả để biến đổi "Điều kiện cho trước" đến một đẳng thức mà từ đó ta dể dàng kết luận được tính chất của tam giác 3) Nhận dạng tam giác đều Ngoài phương pháp đã nêu trên ta có thể giải quyết bài toán theo cách sau Phương pháp sử dụng bất đẳng thức: Gồm 2 bước (áp dụng khi "Điều kiện cho trước" có dạng đẳng thức A = B Bước 1: CM bất đẳng thức hoặc (1) Bước 2: Lập luận để đẳng thức ở (1) xãy ra mà khi đẳng thức (1) xảy ra thì tam giác ABC đều VÍ DỤ MINH HỌA: Ví dụ 1: Tam giác ABC có . Chứng minh rằng ABC vuông Ví dụ 2: Chứng minh rằng nếu thỏa mãn điều kiện thì tam giác đó là tam giác vuông Ví dụ 3: Chứng minh rằng nếu tam giác ABC thoả mãn một trong các điều kiện sau là tam giác cân 1) 2) Ví dụ 4: Chứng minh rằng nếu tam giác ABC thoả mãn một trong các điều kiện sau là tam giác đều 1) 2) 3) 4) Ví dụ 5: Xác định dạng của tam giác ABC biết: 1) 2) 3) 4) Ví dụ 6: Hãy tính các góc của tam giác ABC nếu trong tam giác đó ta có : Ví dụ 7: Tính các góc của tam giác ABC biết rằng trong đó BC = a, AB = c, --------------------------------Hết---------------------------
Tài liệu đính kèm:
 chuyen_de_toan_lop_10_chuyen_de_9_he_thuc_luong_giac_trong_t.doc
chuyen_de_toan_lop_10_chuyen_de_9_he_thuc_luong_giac_trong_t.doc





