Đề cương ôn tập chương III Hình học 11
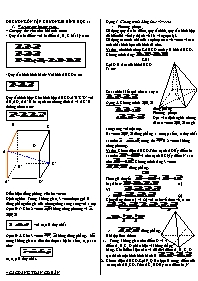
* CÁC DẠNG TOÁN CƠ BẢN
Dạng 1: Chứng minh đẳng thức về vecto
- Phương pháp:
Sử dụng quy tắc ba điểm, quy tắc hbh, quy tắc hình hộp để biến đổi vế này thành vế kia và ngược lại.
Sử dụng các tính chất của ác phép toán về vecto và các tính chất hình học của hình đã cho.
Bạn đang xem tài liệu "Đề cương ôn tập chương III Hình học 11", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ĐỀ CƯƠNG ÔN TẬP CHƯƠNG III HÌNH HỌC 11 Vecto trong không gian: * Các quy tắc cần nhớ khi tính toán: - Quy tắc ba điểm: với ba điểm A, B, C bất kỳ ta có - Quy tắc hình bình hành: Với hbh ABCD ta có Quy tắc hình hộp: Quy tắc hình hộp: Cho hình hộp ABCD.A’B’C’D’ với AB, AD, AA’ là ba cạnh có chung đỉnh A và AC’ là đường chéo ta có: C’ A B C D A’ B’ D’ Điều kiện đồng phẳng của ba vecto: Định nghĩa: Trong không gian, 3 vecto được gọi là đồng phẳng nếu giá của chúng cùng song song với 1 mp Định lý 1: Cho 2 vecto không cùng phương và . , = với m,n là duy nhất Định lý 2: Cho 3 vecto , không đồng phẳng. trong không gian ta đều tìm được 1 bộ ba số m, n, p sao cho: m, n, p là duy nhất. * CÁC DẠNG TOÁN CƠ BẢN Dạng 1: Chứng minh đẳng thức về vecto Phương pháp: Sử dụng quy tắc ba điểm, quy tắc hbh, quy tắc hình hộp để biến đổi vế này thành vế kia và ngược lại. Sử dụng các tính chất của ác phép toán về vecto và các tính chất hình học của hình đã cho. Ví dụ: cho hình chóp S.ABCD có đáy là hbh ABCD. Chứng minh rằng: . Giải Gọi O là tâm của hbhABCD Ta có: So sánh hai kết quả trên ta suy ra . Dạng 2: Chứng minh , đồng phẳng Phương pháp: Dựa vào định nghĩa chứng tỏ cac vecto , có giá song song với một mp. Ba vecto , đồng phẳng ó có cặp số m, n duy nhất sao cho = , trong đó là 2 vecto không cùng phương. Ví dụ: Cho tứ diện ABCD. Trên cạnh AD lấy điểm M sao cho và trên cạnh BC l;ấy điểm N sao cho . Chứng minh rằng 3 vecto đồng phẳng. Giải Theo giả thuyết và Mặt khác: (1) Và => (2) Cộng đẳng thức (1) và (2) với nahu vế theo vế, ta có => đồng phẳng. Bài tập làm thêm: Trong không gian cho điểm O và 4 điểm A, B, C, D phân biệt và không thẳng hàng. CMR điều kiện cần và đủ để 4 điểm A, B, C, D tạo thành một hình bình hành là Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của các cạnh AB, CD. Trên AC, BD lấy các điểm M, N Chứng minh rằng đồng phẳng. Hai đường thẳng vuông góc: Tích vô hướng: Cho tích vô hướng của 2 vecto này trong không gian được xác định bởi: Vecto chỉ phương của đường thẳng: Vectơ được gọi là Vectơ chỉ phương của đường thẳng d nếu giá của nó song song hoặc trùng với đường thẳng d. = Xác định góc giữa hai vecto bằng theo công thức: Góc giữa hai đường thẳng:
Tài liệu đính kèm:
 giao an 11hay.doc
giao an 11hay.doc





