Đề kiểm tra học kỳ I lớp 10 môn Toán chương trình nâng cao
Câu I. (4 điểm)
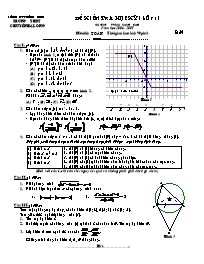
1. Hàm số f(x) = x-1-x+3+ 2, có đồ thị (G).
Đ Dựa vào hình 1, ta tịnh tiến (G) như thế nào để được (G') là đồ thị của một hàm số lẻ?
Đ (G') là đồ thị của hàm số nào dưới đây?
(A) y = x + 2-x - 2
(B) y = x -x + 4
(C) y = x - 2-x + 2
(D) y = x - 3-x + 1+ 3
Bạn đang xem tài liệu "Đề kiểm tra học kỳ I lớp 10 môn Toán chương trình nâng cao", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Sở GD ĐT Quảng Ninh
Trường THPT
chuyên Hạ Long
đề kiểm tra học kỳ I lớp 10
chương trình nâng cao
Năm học 2006 - 2007
Môn thi: Toán Thời gian làm bài: 90 phút Đề 1
----------------------------------------------------------------------------
6
4
2
-2
-5
5
x
y
O
f(x) = ữx-1ờ-ữx+3ờ+2
-1
(G)
Hình 1
Câu I. (4 điểm)
Hàm số f(x) = ữx-1ờ-ữx+3ờ+ 2, có đồ thị (G).
Dựa vào hình 1, ta tịnh tiến (G) như thế nào để được (G') là đồ thị của một hàm số lẻ?
(G') là đồ thị của hàm số nào dưới đây?
(A) y = ữx + 2ờ-ữx - 2ờ
(B) y = ữx ờ-ữx + 4ờ
(C) y = ữx - 2ờ-ữx + 2ờ
(D) y = ữx - 3ờ-ữx + 1ờ+ 3
3
AC
-
EB
+
2
FD
+
FE
(
)
Cho các điểm A, B, C, D, E, F trên hình 2.
Khi đó bằng:
AE
BD
FA
0
-5
x
F
D
C
B
A
O
E
-4
-3
-2
-1
1
2
3
Hình 2
(A) ; (B) ; (C) ; (D)
Cho hàm số y = f(x) = x2 - 2x - 2.
Lập bảng biến thiên của hàm số y = f(x).
Dựa vào bảng biến thiên hãy điền dấu (>, <, =) thích hợp vào ô trống:
;
Cho các hàm số y = x2 + x - 2 có đồ thị là parabol (P) và y = 3x + k có đồ thị là đường thẳng (d).
Hãy ghép mỗi dòng ở cột trái với một dòng ở cột phải để được một khẳng định đúng.
a) Nếu k > -3
b) Nếu -3 < k < -2
c) Nếu k < -3
d) Nếu k = -3
1. thì (P) và (d) không có điểm chung.
2. thì (P) và (d) có một điểm chung.
3. thì (P) và (d) có hai điểm chung phân biệt.
4. thì (P) cắt (d) tại hai điểm nằm ở hai phía khác nhau của trục tung.
5. thì (P) cắt (d) tại hai điểm nằm cùng phía của trục tung.
(Đối với câu I, chỉ cần viết ngay kết quả và không phải giải thích gì thêm)
Câu II. (3 điểm)
E
D
I
C
B
A
Hình 3
Giải phương trình
Giải và biện luận theo m các phương trình sau:
b.
Câu III. (3 điểm)
Trên mặt phẳng toạ độ Oxy, cho ba điểm A(2; 4), B(-1; 1) và C(5; -2).
Tam giác ABC nội tiếp đường tròn (I).
Tìm toạ độ điểm I.
Hai tiếp tuyến của đường tròn (I) tại B và C cắt nhau ở D. Tìm toạ độ điểm D.
Lấy điểm E trên cạnh BC sao cho .
Chứng minh rằng ba điểm A, E, D thẳng hàng.
Hết...
Sở GD ĐT Quảng Ninh
Trường THPT
chuyên Hạ Long
đề kiểm tra học kỳ I lớp 10
chương trình nâng cao
Năm học 2006 - 2007
Môn thi: Toán Thời gian làm bài: 90 phút Đề 2
----------------------------------------------------------------------------
y
x
f(x) = ữx+1ờ-ữx-3ờ+ 2
(G)
1
2
O
Hình 1
Câu I. (4 điểm)
Hàm số f(x) = ữx +1ờ-ữx -3ờ+ 2, có đồ thị (G).
Dựa vào hình 1, ta tịnh tiến (G) như thế nào để được (G') là đồ thị của một hàm số lẻ?
(G') là đồ thị của hàm số nào dưới đây?
(A) y = ữx - 3ờ-ữx + 1ờ
(B) y = ữx ờ-ữx + 4ờ
(C) y = ữx - 2ờ-ữx + 2ờ
(D) y = ữx + 2ờ-ữx - 2ờ
3
BD
-
EB
+
2
FD
+
FE
(
)
Cho các điểm A, B, C, D, E, F trên hình 2.
Khi đó bằng:
AC
BE
ED
0
(A) ; (B) ; (C) ; (D)
-5
x
F
D
C
B
A
O
E
-4
-3
-2
-1
1
2
3
Hình 2
Cho hàm số y = f(x) = x2 + 2x - 1.
Lập bảng biến thiên của hàm số y = f(x).
Dựa vào bảng biến thiên hãy điền dấu (>, <, =) thích hợp vào ô trống:
;
Cho các hàm số y = x2 + 3x - 1 có đồ thị là parabol (P) và y = x + k có đồ thị là đường thẳng (d).
Hãy ghép mỗi dòng ở cột trái với một dòng ở cột phải để được một khẳng định đúng.
a) Nếu k < -2
b) Nếu -2 < k < -1
c) Nếu k = -2
d) Nếu k > -2
1. thì (P) và (d) không có điểm chung.
2. thì (P) và (d) có một điểm chung.
3. thì (P) và (d) có hai điểm chung phân biệt.
4. thì (P) cắt (d) tại hai điểm nằm ở hai phía khác nhau của trục tung.
5. thì (P) cắt (d) tại hai điểm nằm cùng phía của trục tung.
(Đối với câu I, chỉ cần viết ngay kết quả và không phải giải thích gì thêm)
Câu II. (3 điểm)
E
D
I
C
B
A
Hình 3
Giải phương trình
Giải và biện luận theo m các phương trình sau:
a. b.
Câu III. (3 điểm)
Trên mặt phẳng toạ độ Oxy, cho ba điểm A(-2; 4), B(1; 1) và C(-5; -2).
Tam giác ABC nội tiếp đường tròn (I).
Tìm toạ độ điểm I.
Hai tiếp tuyến của đường tròn (I) tại B và C cắt nhau ở D. Tìm toạ độ điểm D.
Lấy điểm E trên cạnh BC sao cho .
Chứng minh rằng ba điểm A, E, D thẳng hàng.
Hết...
đáp án và biểu điểm
đề kiểm tra học kỳ I lớp 10 năm học 2006 - 2007
Chương trình nâng cao
TT
đáp án đề 1
đáp án đề 2
Điểm
I
4đ
Tịnh tiến xuống dưới 2 đv, rồi sang phải 1 đv.
(C)
Tịnh tiến xuống dưới 2 đv, rồi sang trái 1 đv.
(D)
0,5
0,5
1
-3
x
y
O
y = x2 - 2x - 2
(D)
y
x
+Ơ
-Ơ
-1
-2
+Ơ
+Ơ
2
-2
-1
x
y
O
-1
y = x2 + 2x - 1
(B)
1
y
x
+Ơ
-Ơ
1
-3
+Ơ
+Ơ
> , =
(Minh hoạ thêm cho câu I.4)
< , =
(Minh hoạ thêm cho câu I.4)
0,5
0,5
a) -- 3. b) -- 5. c) -- 1. d) -- 2.
a) -- 1. b) -- 5. c) -- 2. d) -- 3.
1
II
3đ
(1)ị3x2 - 9x + 4 = (x-1)2 Û (2x - 1)(x - 3) = 0
Thử lại, được x = 3 là nghiệm.
(1)ị3x2 - 11x + 7 = (x-2)2Û (2x - 1)(x - 3) = 0
Thử lại, được x = 3 là nghiệm.
0,5
0,5
(2) Û
Xét (2a): m = -3,(2a) nghiệm đúng với "xẻR.
m ạ -3, (2a) có một nghiệm x = 1.
Xét (2b): m = 3, (2b) vô nghiệm
m ạ 3, (2b) có một nghiệm x =
KL: Với m = -3, S = R.
Với m = 3, S = {1}.
Với m ạ 3 và m ạ -3, S = .
(S - tập nghiệm của phương trình (2))
(2) Û
Xét (2a): m = -3,(2a) nghiệm đúng với "xẻR
m ạ -3, (2a) có một nghiệm x = -1.
Xét (2b): m = 3, (2b) vô nghiệm
mạ3, (2b) có một nghiệm x =
KL: Với m = -3, S = R.
Với m = 3, S = {-1}.
Với m ạ 3 và m ạ -3, S = .
(S - tập nghiệm của phương trình (2))
0,25
0,5
0,25
Nếu m = 0, (3) vô nghiệm.
Nếu m ạ 0.
Với điều kiện x ạ -1,
(3) Û x2 + 2(1 - m)x + m2 - 2m - 3 = 0 (D' = 4)
Û x = m + 1 hoặc x = m - 3
Xét các điều kiện:
m + 1 ạ -1 Û m ạ -2; m - 3 ạ -1 Û m ạ 2.
KL: Với m = 0, (3) vô nghiệm.
Với m = -2, (3) có nghiệm x = m-3 = -5
Với m = 2, (3) có nghiệm x = m + 1 = 3
Với m ạ 0, m ạ -2 và m ạ 2, (3) có hai nghiệm x = m + 1 và x = m - 3.
0,5
0,25
0,25
III
3đ
I(x; y) - tâm đường tròn ngoại tiếp DABC
Û
Û
Û Giải hệ, ta được I
I(x; y) - tâm đường tròn ngoại tiếp DABC
Û
Û
Û Giải hệ, ta được I
0,5
0,5
Gọi D(x; y)
BD = (x + 1; y - 1); CD = (x - 5; y + 2)
BI = ; CI =
D-giao hai tiếp tuyến của (I) tại B, C khi và chỉ khi:
Û Giải hệ, ta được D
Gọi D(x; y)
BD = (x - 1; y - 1); CD = (x + 5; y + 2)
BI = ; CI =
D-giao hai tiếp tuyến của (I) tại B, C khi và chỉ khi:
Û Giải hệ, ta được D
0,25
0,5
0,25
AB2 = 18; AC2 = 45. Gọi E(x; y)
BE
=
2
7
BC
. Suy ra: lại có
BE
= (x+1; y -1),
BC
= (6;
-3)
AE
=
-9
7
;
-27
7
(
)
,
AD
=
-9
2
;
-27
2
(
)
nên Suy được E =
4
2
-2
-4
-6
-8
-10
-5
5
D
I
5
2
;
1
2
(
)
C(5; -2)
B(-1; 1)
A(2, 4)
E
O
x
y
Do vậy A, E, D thẳng hàng.
AE
=
2
7
AD
AB2 = 18; AC2 = 45. Gọi E(x; y)
BE
=
2
7
BC
. Suy ra: lại có
BE
= (x-1; y -1),
BC
= (-6;
-3)
AE
=
9
7
;
-27
7
(
)
,
AD
=
9
2
;
-27
2
(
)
nên Suy được E =
4
2
-2
-4
-6
-8
-10
-5
5
C(-5; -2)
I
-
5
2
;
1
2
(
)
A(-2, 4)
E
D
x
y
O
B (1; 1)
Do vậy A, E, D thẳng hàng.
AE
=
2
7
AD
0,75
0,25
Tài liệu đính kèm:
 De HK1nang cao.doc
De HK1nang cao.doc





