Đề kiểm tra môn Đại số 10 - Học kỳ I

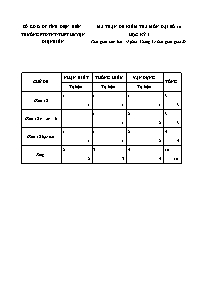
SỞ GD & ĐT TỈNH ĐIỆN BIÊN
TRƯỜNG PTDTNT-THPT HUYỆN ĐIỆN BIÊN
MA TRẬN ĐỀ KIỂM TRA MÔN ĐẠI SỐ 10 
 HỌC KỲ I
Thời gian làm bài: 45 phút, không kể thời gian giao đề
CHỦ ĐỀ
NHẬN BIẾT
THÔNG HIỂU
VẬN DỤNG
TỔNG
Tự luận
Tự luận
Tự luận
Hàm số 
1
1
1
3
1
1
1
3
Hàm số y = ax + b
1
2
3
1
2
3
Hàm số bậc hai
1
1
2
4
1
1
2
4
Tổng
2
3
5
10
2
3
5
10
SỞ GD & ĐT TỈNH ĐIỆN BIÊN
TRƯỜNG PTDTNT-THPT 
HUYỆN ĐIỆN BIÊN
ĐỀ KIỂM TRA MÔN ĐẠI SỐ 10 - HỌC KỲ I
Thời gian làm bài: 45 phút
ĐỀ I:
Câu 1 (3 điểm): Tìm tập xác định của các hàm số sau:
 	a) 	b) 	c) 
Câu 2 (2 điểm): Xác định hệ số a, b của hàm số y = ax + b, biết đồ thị hàm số đi qua A(-1; 2) và B(6; 0)
Câu 3 (3 điểm): Lập bảng biến thiên và vẽ đồ thị hàm số: y = x2 - 2x - 3
Câu 4 (2 điểm): Tìm tọa độ giao điểm của đường thẳng có phương trình: y = x - 3 với Parabol có phương trình: y = 2x2 - 5x + 1
ĐÁP ÁN ĐỀ I:
Câu
Ý
Đáp án
Điểm
1
a
ĐKXĐ: 
0,5
1
TXĐ: 
0,5
b
ĐKXĐ: 	
0,5
1
TXĐ: 
0,5
c
ĐKXĐ: 	
0,5
1
TXĐ: 
0,5
2
Vì đồ thị hàm số đi qua A(1; -2) và B(0; 4) nên ta có: 
1
Giải hệ trên tìm được . Vậy hàm số cần tìm là: y = 4x + 6
1
3
0,5
a > 0. Vậy hàm số đồng biến trên khoảng ;
 nghịch biến trên khoảng
0,5
Bảng biến thiên: 
x
 1 
y
 -4
0,5
Đồ thị hàm số : y = x2 - 2x - 3 là một Parabol có:
Đỉnh I(1; -4) và nhận đường thẳng x = 1 làm trục đối xứng
0,5
Đồ thị giao với trục tung tại điểm (0; -3)
 giao với trục hoành tại điểm (-1; 0) và (3; 0)
 điểm (2; -3) thuộc đồ thị hàm số
Đồ thị:
 y
 -1 O 1 2 3 x
 -3
 -4
1
4
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
2x2 - 5x + 1 = x - 3 ó 2x2 - 6x + 4 = 0 ó
1
Thay x = 1 vào hàm số y = x -3 ta có y = -2
Thay x = 2 vào hàm số y = x -3 ta có y = -1
Vậy hai đồ thị giao nhau tại điểm (1; -2) và (2; -1)
1
SỞ GD & ĐT TỈNH ĐIỆN BIÊN
TRƯỜNG PTDTNT-THPT 
HUYỆN ĐIỆN BIÊN
ĐỀ KIỂM TRA MÔN ĐẠI SỐ 10 - HỌC KỲ I
Thời gian làm bài: 45 phút
ĐỀ II:
Câu 1 (3 điểm): Tìm tập xác định của các hàm số sau:
	a) 	b) 	c) 
Câu 2 (2 điểm): Xác định hệ số a, b của hàm số y = ax + b, biết đồ thị hàm số đi qua A(-2; 2) và song song với đường thẳng y = -2x – 3
Câu 3 (3 điểm): Lập bảng biến thiên và vẽ đồ thị hàm số: y = -x2 - 2x + 3
Câu 4 (2 điểm): Tìm tọa độ giao điểm của đường thẳng có phương trình: y = x + 1 với Parabol có phương trình: y = x2 - 5x + 1
ĐÁP ÁN ĐỀ II:
Câu
Ý
Đáp án
Điểm
1
a
ĐKXĐ: 
0,5
1
TXĐ: 
0,5
b
ĐKXĐ: 	
0,5
1
TXĐ: 
0,5
c
ĐKXĐ: 	
0,5
1
TXĐ: 
0,5
2
Vì đồ thị hàm số đi qua A(-2; 2) và song song với đường thẳng 
y = -2x – 3 nên ta có: 
1
Giải hệ trên tìm được . Vậy hàm số cần tìm là: y = -2x - 2
1
3
0,5
a > 0. Vậy hàm số nghịch biến trên khoảng;
 đồng biến trên khoảng
0,5
Bảng biến thiên: 
x
 -1 
y
 4 
0,5
Đồ thị hàm số : y = -x2 - 2x + 3 là một Parabol có:
Đỉnh I(-1; 4) và nhận đường thẳng x = -1 làm trục đối xứng
0,5
Đồ thị giao với trục tung tại điểm (0; 3)
 giao với trục hoành tại điểm (1; 0) và (-3; 0)
 điểm (-2; 3) thuộc đồ thị hàm số
Đồ thị:
 y
 4 
 3 
 -3 -1 O 1 x
1
4
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
x2 - 5x + 1= x + 1 ó x2 - 6x = 0 ó
1
Thay x = 0 vào hàm số y = x + 1 ta có y = 1
Thay x = 6 vào hàm số y = x + 1 ta có y = 7
Vậy hai đồ thị giao nhau tại điểm (0; 1) và (6; 7)
1
SỞ GD & ĐT TỈNH ĐIỆN BIÊN
TRƯỜNG PTDTNT-THPT 
HUYỆN ĐIỆN BIÊN
ĐỀ KIỂM TRA MÔN ĐẠI SỐ 10 - HỌC KỲ I
Thời gian làm bài: 45 phút
ĐỀ III:
Câu 1 (3 điểm): Tìm tập xác định của các hàm số sau:
 	a) 	b) 	c) 
Câu 2 (2 điểm): Xác định hệ số a, b của hàm số y = ax + b, biết đồ thị hàm số đi qua A(1; -2) và và vuông góc với đường thẳng y = -x – 3
Câu 3 (3 điểm): Lập bảng biến thiên và vẽ đồ thị hàm số: y = x2 - 2x - 3
Câu 4 (2 điểm): Tìm tọa độ giao điểm của đường thẳng có phương trình: y = x + 1 với Parabol có phương trình: y = x2 - 5x + 1
ĐÁP ÁN ĐỀ III:
Câu
Ý
Đáp án
Điểm
1
a
ĐKXĐ: 
0,5
1
TXĐ: 
0,5
b
ĐKXĐ: 	
0,5
1
TXĐ: 
0,5
c
ĐKXĐ: 	
0,5
1
TXĐ: 
0,5
2
Vì đồ thị hàm số đi qua A(1; -2) và vuông góc với đường thẳng 
y = -x – 3 nên ta có: 
1
Giải hệ trên tìm được . Vậy hàm số cần tìm là: y = x - 3
1
3
0,5
a > 0. Vậy hàm số đồng biến trên khoảng ;
 nghịch biến trên khoảng
0,5
Bảng biến thiên: 
x
 1 
y
 -4
0,5
Đồ thị hàm số : y = x2 - 2x - 3 là một Parabol có:
Đỉnh I(1; -4) và nhận đường thẳng x = 1 làm trục đối xứng
0,5
Đồ thị giao với trục tung tại điểm (0; -3)
 giao với trục hoành tại điểm (-1; 0) và (3; 0)
 điểm (2; -3) thuộc đồ thị hàm số
Đồ thị:
 y
 -1 O 1 2 3 x
 -3
 -4
1
4
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
x2 - 5x + 1= x + 1 ó x2 - 6x = 0 ó
1
Thay x = 0 vào hàm số y = x + 1 ta có y = 1
Thay x = 6 vào hàm số y = x + 1 ta có y = 7
Vậy hai đồ thị giao nhau tại điểm (0; 1) và (6; 7)
1
SỞ GD & ĐT TỈNH ĐIỆN BIÊN
TRƯỜNG PTDTNT-THPT 
HUYỆN ĐIỆN BIÊN
ĐỀ KIỂM TRA MÔN ĐẠI SỐ 10 - HỌC KỲ I
Thời gian làm bài: 45 phút
CHỦ ĐỀ
NHẬN BIẾT
THÔNG HIỂU
VẬN DỤNG
TỔNG
Tự luận
Tự luận
Tự luận
ĐẠI SỐ
Mệnh đề - Tập hợp
1
1
2
0,5
0,5
1
Hàm số bâc nhất 
và hàm số bậc hai
1
1
2
0,5
1,5
2
Phương trình và hệ phương trình
1
1
2
1
1
2
Bất đẳng thức. Bất phương trình
1
1
1
1
HÌNH HỌC
Vectơ
1
1
2
1
1
2
Tích vô hướng của hai vectơ và ứng dụng
1
1
2
1
1
2
Tổng
5
4
2
11
4
4
2
10
SỞ GD & ĐT TỈNH ĐIỆN BIÊN
TRƯỜNG PTDTNT-THPT 
HUYỆN ĐIỆN BIÊN
ĐỀ KIỂM TRA MÔN ĐẠI SỐ 10 - HỌC KỲ I
Thời gian làm bài: 45 phút
ĐỀ BÀI 
Câu 1: (1điểm) Xác định các tập hợp sau và biểu diễn trên trục số:
	a) 	b) 
Câu 2: (2 điểm) 
	a) Lập bảng biến thiên và vẽ đồ thị hàm số: y = -x2 + 2x - 2
b) Tìm tọa độ giao điểm của đường thẳng có phương trình: y = -x với Parabol có phương trình: y = -x2 + 2x - 2
Câu 3: (2 điểm) Giải các phương trình sau:
	a) 	b) 
Câu 4: (1 điểm) Cho a, b là các số dương, chứng minh rằng: 
Câu 5: (4 điểm) Cho 3 điểm A(2;4), B(1;2), C(6;2)
	a) Tìm tọa độ các vectơ 
	b) Chứng minh rằng tam giác ABC vuông tại A. Tính diện tích tam giác ABC. 
	c) Cho AH vuông góc với BC tại H, tìm tọa độ H?
ĐÁP ÁN - 
Câu
Ý
Đáp án
Điểm
1
a
 - 2 3
0,5
b
 3 4 5 6 
0,5
2
a
 . Ta có: a < 0. Vậy hàm số nghịch biến trên khoảng ;
 đồng biến trên khoảng
0,25
1,5
Bảng biến thiên: 
x
 1 
y
 -1 
0,25
Đồ thị hàm số : y = -x2 + 2x - 2 là một Parabol có:
Đỉnh I(1; -1) và nhận đường thẳng x = 1 làm trục đối xứng
0,25
Đồ thị giao với trục tung tại điểm (0; -2) và không giao với trục hoành Điểm (2; -2), (-1; -5) và (3; -5) thuộc đồ thị hàm số
0,25
Đồ thị: y
 O 1 2 3 x 
 -2
 -5
0,5
b
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
-x2 + 2x - 2 = -x ó -x2 + 3x - 2 = 0 ó
0,25
0,5
Thay x = 1 vào hàm số y = -x ta có y = -1
Thay x = 2 vào hàm số y = -x ta có y = -2
Vậy hai đồ thị giao nhau tại điểm (1; -1) và (2; -2)
0,25
3
a
Ta có: 
+) Khi x : (1) => 2x – 3 = -5(2 + x) 7x = -7 x = -1 (loại) 
+) Khi x :(1) => -2x + 3 = -5(2 + x) x = (thỏa mãn x )
Vậy phương trình có một nghiệm x = 
0,5
1
0,5
b
c) ĐKXĐ: . Ta có: 
Cả hai giá trị trên đều thỏa mãn phương trình, vậy phương trình có hai nghiệm x = 1 và x = 
0,5
1
0,5
4
Bất đẳng thức trên luôn đúng với mọi số dương a và b
1
5
a
 ;;
1
4
b
Ta có: ;. ;
Ta có: = (-1).4 +(-2).(-2) = 0 => .
Vậy tam giác ABC vuông tại A 
=> Diện tích tam giác ABC là 
1
1
c
Gọi tọa độ điểm H là (x; y). Vì AH vuông góc với BC tại H nên: 
. 
Mặt khác cùng phương với nên . 
Vậy H(2; 2)