Giáo án Phụ đạo hình học 10 chương I tuần I

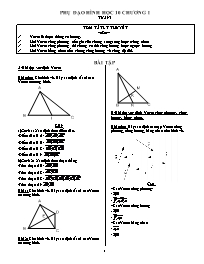
PHỤ ĐẠO HÌNH HỌC 10 CHƯƠNG I
TUẦN I
TÓM TẮT LÝ THUYẾT
--oOo---
Vectơ là đoạn thẳng có hướng.
Hai Vectơ cùng phương nếu giá của chúng song song hoặc trùng nhau
Hai Vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng
Hai Vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
BÀI TẬP
A-Bài tập xác định Vectơ 
Bài mẫu: Cho hình vẽ. Hãy xác định tất cả các Vectơ có trong hình.
Giải:
a)Cách 1: Xác định theo điểm đầu.
-Điểm đầu là A: 
-Điểm đầu là B: 
-Điểm đầu là C: 
-Điểm đầu là I: 
b)Cách 2: Xác định theo đoạn thẳng
-Trên đoạn AB: 
-Trên đoạn AC: 
-Trên đoạn BC: 
-Trên đoạn AI: 
Bài 1: Cho hình vẽ. Hãy xác định tất cả các Vectơ có trong hình.
Bài 2: Cho hình vẽ. Hãy xác định tất cả các Vectơ có trong hình.
B-Bài tập xác định Vectơ cùng phương, cùng hướng, bằng nhau.
Bài mẫu: Hãy xác định các cặp Vectơ cùng phương, cùng hướng, bằng nhau trên hình vẽ.
Giải:
*Các Vectơ cùng phương:
-
-
*Các Vectơ cùng hướng
-
-
*Các Vectơ bằng nhau
-
-
Bài 1: Hãy xác định các cặp Vectơ cùng phương, cùng hướng, bằng nhau trên hình vẽ.
Bài 2: Cho hình bình hành ABCD tâm O. I và J lần lượt là trung điểm của BC và AD
-Xác định các Vectơ cùng phương với Vectơ 
-Xác định các Vectơ cùng hướng với Vectơ 
-Xác định các Vectơ bằng nhau với Vectơ 
C-Bài tập chứng minh
Bài mẫu: Cho tam giác ABC gọi I và J lần lượt là trung điểm của AB và AC. Chứng minh rằng là đường trung bình của cạnh BC khi và chỉ khi 
Giải:
+Vế trái : là đường trung bình của BC
Theo tính chất đường trung bình ta có
+Vế phải: 
Theo định nghĩa hai Vectơ bằng nhau ta có
Bài 1: Chứng minh rằng ABCD là hình bình hành khi và chỉ khi 
Bài 2: Chứng minh rằng I là trung điểm của BC khi và chỉ khi 
Bài 3: Cho tứ giác ABCD. Gọi M, N, P ,Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh