Giáo án Toán Đại số Lớp 10 - Chương IV, Bài 1: Bất đẳng thức
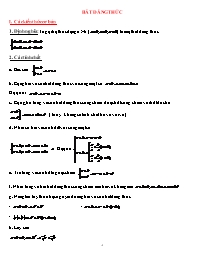
1. Định nghĩa: Ta gọi hệ thức dạng a > b ( ) là một bất đẳng thức
2. Các tính chất
a. Bắc cầu:
b. Cộng hai vế của bất đẳng thức với cùng một số:
Hệ quả 1:
c. Cộng, trừ từng vế của bất đẳng thức cùng chiều được bđt cùng chiều với bđt đã cho
( lưu ý: không có tính chất trừ vế với vế )
d. Nhân cả hai vế của bddt với cùng một số
Hệ quả:
e. Trừ từng vế của bđt ngược chiều:
Bạn đang xem tài liệu "Giáo án Toán Đại số Lớp 10 - Chương IV, Bài 1: Bất đẳng thức", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
BẤT ĐẲNG THỨC I. Các kiến thức cơ bản 1. Định nghĩa: Ta gọi hệ thức dạng a > b () là một bất đẳng thức 2. Các tính chất a. Bắc cầu: b. Cộng hai vế của bất đẳng thức với cùng một số: Hệ quả 1: c. Cộng, trừ từng vế của bất đẳng thức cùng chiều được bđt cùng chiều với bđt đã cho ( lưu ý: không có tính chất trừ vế với vế ) d. Nhân cả hai vế của bddt với cùng một số Hệ quả: e. Trừ từng vế của bđt ngược chiều: f. Nhân từng vế hai bất đẳng thức cùng chiều mà hai vế không âm: g. Nâng lên lũy thừa bậc nguyên dương hai vế của bất đẳng thức: - - - h. Lấy căn Hệ quả: i. Lấy nghịch đảo hai vế và đổi chiều bđt nếu hai vế cùng dấu - - II. Các hằng đẳng thức 1. 2. 3. 4. 5. III. Các bổ đề hay sử dụng 1. 2. 3. 4. 5. IV. Các dạng toán Dạng 1: Dùng định nghĩa và các phép biến đổi tương đương - Để chứng minh: ta xét A – B và chứng minh Bài 1: Cho ba số a, b, c bất kỳ, chứng minh bất đẳng thức sau: Lời giải Dấu “ = ” xảy ra Bài 2: Cho ba số a, b, c bất kỳ, chứng minh rằng: Lời giải Dấu “ = ” xảy ra Bài 3: Chứng minh rằng: Lời giải Bài 4: Cho ba số a, b, c thỏa mãn: Lời giải Xét hiệu: Bài 5: Chứng minh rằng: với a, b, c > 0 Lời giải Xét hiệu: Bài 6: Chứng minh rằng nếu thì Lời giải Xét hiệu: Bài 7: Chứng minh rằng nếu ta luôn có: Lời giải Dạng 2: Dùng các phép biến đổi tương đương - Ta biến đổi các bất đẳng thức cần chứng minh tương đường với BĐT đúng hoặc BĐT đã được chứng minh là đúng - Nếu , với C < D luôn đúng Bài 1: Cho a, b, c, d, e là các số thực, CMR: a. b. c. d. Lời giải a. b. c. d. Bài 2: Cho ba số thỏa mãn: abc = 1 và a. Chứng minh rằng: b. Chứng minh răng luôn tồn tại 1 trong ba số a, b, c nhỏ hơn 1 Lời giải a. Ta có: và Từ (1)(2) ta có điều phải chứng minh b. Giả sử tồn tại cả ba số a, b, c lớn hơn 1 ( mâu thuẫn với giả thiết ) Vậy luôn tồn tại 1 số nhỏ hơn 1. Bài 3: Chứng minh bất đẳng thức sau: Lời giải Bài 4: Chứng minh rằng: Lời giải Ta có: Tương tự: . Vậy Lại có: Cộng vế với vế ba bất đẳng thức ta được: Bài 5: [ Vào 10, ĐHSP TPHCM năm 2007 – 2008 ]. Cho a, b, c > 0. Chứng minh rằng: Lời giải Bài 6: [ Vào 10 Thanh Hóa, năm 2007 – 2008 ]. Chứng minh rằng: Lời giải Bài 7: [ HSG – 1994 - 1995 ] Chứng minh rằng với mọi số thực ta có Lời giải Bài 8: [ Chuyên An Giang năm 2010 - 2011 ] Cho Lời giải Do Đặt Bài 9: [ Vào 10 chuyên KHTN, ĐHQGHN, năm 2000 – 2001 ] Cho hai số thực Lời giải Bài 10: [ Lớp 9 ] Cho các số thực a,b. Chứng minh rằng: Lời giải Ta có: - Ta có: Dạng 3: Bất đẳng thức dạng nghịch đảo ( Cô si cộng mẫu ) - - - Bài 1: Cho a, b, c > 0. CMR: Lời giải Áp dụng bất đẳng thức dạng: ( tự chứng minh bđt) Cộng vế các bất đẳng thức trên ta được: Bài 2: Cho a, b, c > 0. CMR: Lời giải Áp dụng bất đẳng thức dạng: Cộng vế ba bất đẳng thức trên ta được: Bài 3: Cho a, b, c > 0. CMR: Lời giải Áp dụng bất đẳng thức: Ta được: Bài 4: Cho a, b, c > 0 thỏa mãn: Tìm GTLN của Lời giải Cách 1: Cách 2: Áp dụng bất đẳng thức: Tương tự: Cộng ba vế của bất đẳng thức ta được: Bài 5: Cho a, b, c > 0. Chứng minh rằng Lời giải Áp dụng bất đẳng thức: Bài 6: Cho a, b, c > 0 thỏa mãn: a + b + c = 1. Tìm GTNN: Lời giải Lại có: Cộng theo vế ba bất đẳng thức: BÀI TẬP VẬN DỤNG: Bài 1: Cho a, b, c > 0 . Chứng minh rằng: Lời giải Ta có: Lại có: Từ (1)(2) ta có điều phải chứng minh. Bài 2: Cho a, b, c > 0 . Chứng minh rằng: Lời giải Ta có: Cộng vế với vế các bất đẳng thức ta được đpcm Bài 3: Cho a, b, c > 0 . Chứng minh rằng: Lời giải Dạng 4: Dùng các bất đẳng thức phụ - - - - - - Bài 1: Cho hai số a và b thỏa mãn: a + b = 1. Chứng minh rằng: Lời giải Ta có: Từ: Lại có: Từ (1)(2) Bài 2: Cho a + b > 1 . Chứng minh rằng: Lời giải Từ Có tiếp: Bài 3: Chứng minh rằng: Lời giải Ta có: Áp dụng: Bài 4: Cho a, b, c, d, > 0 và abcd = 1. CMR: Lời giải Ta có: Từ : Có: Vậy Lại có: Bài 5: Cho . CMR: Lời giải Lại có: Bài 6: Cho . CMR: Lời giải Ta có: Bài 7: Cho . CMR: Lời giải Có: Lại có: Bài 8: Cho . a. CMR: b. Lời giải a. Ta có: b. Theo chứng minh trên: Bài 9: Cho thỏa mãn: . Chứng minh rằng: Lời giải Ta có: Áp dụng ta được: Mà: Bài 10: Cho thỏa mãn: . Chứng minh rằng: Lời giải Áp dụng ta có: Tương tự: Cộng vế các bất đẳng thức trên ta được điều phải chứng minh. Bài 11: Cho . Chứng minh rằng: Lời giải Chứng minh: Áp dụng: Cộng vế các bất đẳng thức thức ta được điều phải chứng minh. Bài 12: Cho . Tìm GTNN: Lời giải Ta có: Thật vậy Hoặc: Áp dụng: Cộng vế ba bất đẳng thức ta được: Bài 13: Cho . Tìm GTNN: Lời giải . mà: Áp dụng: Tương tự ta có: DẠNG 5: PHƯƠNG PHÁP PHẢN CHỨNG - Muốn chứng minh bất đẳng thức đúng, ta giả sử là sai, tức là A < B là đúng - Sau đó chứng minh A < B là sai là đúng Bài 1: Cho . CMR: Lời giải Giả sử , bình phương hai vế ta được: Mặt khác ta lại có: Mà Điều này mâu thuẫn với (1) nên Bài 2: Với mọi số thực a, b, c hãy chứng tỏ: . Lời giải Giả sử: Vậy điều giả sử là sai Bài 3: Cho: . Giả sử Bài 4: Cho các số thực có ít nhất 1 trong ba bất đẳng thức sau là sai Lời giải Giả sử cả ba bất đẳng thức trên đều đúng, nhân chúng với nhau theo vế, ta được: Mặt khác, do nên a và Tương tự: Do đó: ( mâu thuẫn ). Vậy ta có đpcm Bài 5: [ Chuyên Thái Bình: năm 2007 – 2008 ] Cho các số thực a, b, c thỏa mãn: Lời giải Giả sử khi đó: Kết hợp với gỉa thiết: ( mâu thuẫn ) Bài 6: [ Chuyên Lam Sơn Thanh Hóa: năm 2007 – 2008 ] Cho các số thực a, b, c thỏa mãn: Chứng minh rằng cả ba số a, b, c đều dương Lời giải Giả sử ba số a, b, c có 1 số không dương. Không mất tính tổng quát, ta giả sử: Mà lại có: Lại có: Từ giả thiết thứ hai: ab + bc + ca > 0, ta có: Vì thế abc < 0 ( mâu thuẫn ). Đpcm Bài 7: Cho ba số a, b, c đôi một khác nhau. CMR: Tồn tại một trong các số 9ab, 9bc, 9ca nhỏ hơn Lời giải Giả sử: Theo đầu bài: a, b, c đôi một khác nhau nên: Từ (1)(2) ta thấy mâu thuẫn nên đpcm. Bài 8: [ Chuyên HCM năm 2006 – 200 7 ] . Cho hai số dương x, y thỏa mãn: Lời giải Do x, y dương Giả sử: do Do đó (*) không thể xảy ra Bài 9: Cho cặp số (x; y) thỏa mãn các điều kiện sau: Lời giải Ta đi chứng minh: Giả sử , khi đó +) +) Do đó nếu . Mà ( mâu thuẫn với 2) Ta đi chứng minh ( tương tự chứng minh ) Bài 10: [ Olympic Toán Ireland năm 1997 ] Cho Lời giải +) Nếu 1 trong ba số bằng 0 thì bất đẳng thức được chứng minh Ta xét: a, b, c > 0 Giả sử ngược lại: Tương tự ta có: Lại có: Từ (1)(2) ( mâu thuẫn với giả thiết ) nên điều giả sử là sai Bài 11: Cho a, b, c là các số thực dương thỏa mãn . Chứng minh rằng có ít nhất hai trong số các bất đẳng thức sau đúng: Lời giải Ta có: Đặt Ta phải chứng minh có ít nhất hai trong ba bất đẳng thức sau đúng: Giả sử có ít nhất 2 trong 3 bất đẳng thức sau là sai, chẳng hạn: Cộng vế hai bất đẳng thức: Từ giả thiết: Bài 12: Cho bốn số a, b, c, d thỏa mãn điều kiện: . Chứng minh rằng có ít nhất một trong các bđt sau là sai: Lời giải Giả sử hai bđt trên đều đúng Theo giả thiết:
Tài liệu đính kèm:
 giao_an_toan_dai_so_lop_10_chuong_iv_bai_1_bat_dang_thuc.docx
giao_an_toan_dai_so_lop_10_chuong_iv_bai_1_bat_dang_thuc.docx





