Trắc nghiệm Đại số 10 - Chương IV: Bất đẳng thức – Bất phương trình

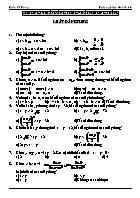
3. Cho m, n > 0. Bất đẳng thức (m + n)  4mn tương đương với bất đẳng thức nào sau đây.
a) n(m–1)2 + m(n–1)2  0 b) (m–n)2 + m + n  0
c) (m + n)2 + m + n  0 d) Tất cả đều đúng.
4. Với mọi a, b  0, ta có bất đẳng thức nào sau đây luôn đúng?
a) a – b < 0="" b)="" a2="" –="" ab="" +="" b2="">< 0="" c)="" a2="" +="" ab="" +="" b2=""> 0 d) Tất cả đều đúng
11 trang
phamhung97 Lượt xem
2698
1 Download
Bạn đang xem tài liệu "Trắc nghiệm Đại số 10 - Chương IV: Bất đẳng thức – Bất phương trình", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHƯƠNG IV: BẤT ĐẲNG THỨC – BẤT PHƯƠNG TRÌNH
I. BẤT ĐẲNG THỨC
Tìm mệnh đề đúng: 
	a) a 
	c) a < b Ù c < d  Þ   ac < bd 	d) Cả a, b, c đều sai. 
Suy luận nào sau đây đúng:
	a) Þ ac > bd	b) Þ 
	c) Þ a – c > b – d	d) Þ ac > bd
Cho m, n > 0. Bất đẳng thức (m + n) ³ 4mn tương đương với bất đẳng thức 	nào sau đây.
	a) n(m–1)2 + m(n–1)2 ³ 0	b) (m–n)2 + m + n ³ 0
	c) (m + n)2 + m + n ³ 0 	d) Tất cả đều đúng.
Với mọi a, b ¹ 0, ta có bất đẳng thức nào sau đây luôn đúng?
	a) a – b 0	d) Tất cả đều đúng
Với hai số x, y dương thoả xy = 36, bất đẳng thức nào sau đây đúng?
	a) x + y ³ 2 = 12	b) x + y ³ 2 = 72 
	c) > xy = 36	d) Tất cả đều đúng
Cho hai số x, y dương thoả x + y = 12, bất đẳng thức nào sau đây đúng?
	a) 2 £ xy = 12	b) xy < = 36
	c) 2xy £ x2 + y2 	d) Tất cả đều đúng
Cho x ³ 0; y ³ 0 và xy = 2. Gía trị nhỏ nhất của A = x2 + y2 là:
	a) 2	b) 1	c) 0	d) 4
Cho a > b > 0 và . 
	Mệnh đề nào sau đây đúng ? 
	a) x > y 	b) x < y 	
	c) x = y 	d) Không so sánh được 
Cho các bất đẳng thức: (I) ≥ 2 ;	
	 (II) ≥ 3 ;
	 (III) ≥ (với a, b, c > 0). 
	Bất đẳng thức nào trong các bất đẳng thức trên là đúng:
	a) chỉ I đúng 	b) chỉ II đúng 	c) chỉ III đúng 	d) I,II,III đều đúng 
Cho DABC và P = . Mệnh đề nào sau đây đúng ? 
	a) 0 < P < 1 	b) 1 < P < 2 	c) 2 < P < 3 	d) kết quả khác.
Cho a, b > 0 và ab > a + b. Mệnh đề nào sau đây đúng ? 
	a) a + b = 4 	b) a + b > 4 	c) a + b < 4 	d) kết quả khác. 
Cho a <  b < c < d và x = (a+b)(c+d), y = (a+c)(b+d), z = (a+d)(b+c). Mệnh 	đề nào sau đây là đúng ? 
	a) x < y < z 	b) y < x < z 	c) z < x < y 	d) x < z < y 
Trong các mệnh đề sau đây với a, b, c, d > 0, tìm mệnh đề sai : 
	a) < 1 Þ < 	
	b) > 1 Þ > 
	c) < 	
	d) Có ít nhất một trong ba mệnh đề trên là sai 
Hai số a, b thoả bất đẳng thức thì: 
	a) a b 	c) a = b 	d) a ≠  b 
Cho x, y, z > 0 và xét ba bất đẳng thức:
	(I)  x3 + y3 + z3 ≥ 3 x y z 
	(II)  
	(III)  ≥ 3 
	Bất đẳng thức nào là đúng ?
	a) Chỉ I đúng 	b) Chỉ I và III đúng c) Chỉ III đúng 	d) Cả ba đều đúng 
II. BẤT PHƯƠNG TRÌNH MỘT ẨN
Bất phương trình nào sau đây tương đương với bất phương trình x + 5 > 0?
	a) (x – 1)2 (x + 5) > 0	b) x2 (x +5) > 0
	c) (x + 5) > 0	d) (x – 5) > 0
Bất phương trình: 2x + < 3 + tương đương với: 
	a) 2x < 3	b) x < và x ¹ 2	c) x < 	d) Tất cả đều đúng
Bất phương trình: (x+1) ³ 0 tương đương với bất phương trình:
	a) (x–1) ³ 0 	b) ³ 0 
	c) ³ 0 	d) ³ 0 
Khẳng định nào sau đây đúng?
	a) x2 £ 3x Û x £ 3	b) < 0 Û x £ 1
	c) ³ 0 Û x – 1 ³ 0 	d) x + ³ x Û ³ 0
Cho bất phương trình: > 1   (1). Một học sinh giải như sau:
	(1) 
	Hỏi học sinh này giải đúng hay sai ? 
	a) Đúng 	b) Sai 
Cho bất phương trình : .( m x – 2 ) < 0   (*). Xét các mệnh đề sau:
	(I)  Bất phương trình tương đương với mx – 2 < 0.
	(II) m ≥  0 là điều kiện cần để mọi x < 1 là nghiệm của bất phương trình (*)	(III) Với m < 0, tập nghiệm của bất phương trình là < x < 1.
	Mệnh đề nào đúng ?
	a) Chỉ I 	b) Chỉ III 	c) II và III 	d) Cả I, II, III 
Cho bất phương trình: m3(x + 2) ≤  m2(x – 1). Xét các mệnh đề sau:
	(I)   Bất phương trình tương đương với x(m – 1) ≤  –(2m + 1).
	(II)  Với m = 0, bất phương trình thoả "x Î  R.
	(III) Giá trị của m để bất phương trình thoả " x  ≥  0 là  ≤  m v  m = 0.
	Mệnh đề nào đúng?
	a) Chỉ (II) 	b) (I) và (II) 	c) (I) và (III) 	d) (I), (II) và (III) 
Tập nghiệm của bất phương trình > là gì?
	a) Æ	b) [ 2006; +¥)	c) (–¥; 2006)	d) {2006}
Bất phương trình 5x – 1 > + 3 có nghiệm là:
	a) "x	b) x 	d) x > 
Với giá trị nào của m thì bất phương trình mx + m < 2n vô nghiệm?
	a) m = 0	b) m = 2	c) m = –2	d) m ÎÂ
Nghiệm của bất phương trình £ 1 là:
	a) 1 £ x £ 3	b) –1 £ x £ 1	c) 1 £ x £ 2	d) –1 £ x £ 2
Bất phương trình > x có nghiệm là:
	a) x 	b) x 
	c) x Î Â	d) Vô nghiệm
Tập nghiệm của bất phương trình < 1 là:
	a) (–¥;–1)	b) c) x Î (1;+¥)	d) x Î (–1;1)
x = –2 là nghiệm của bất phương trình nào sau đây?
	a) 0	
	c) < 0	d) < x
Tập nghiệm của bất phương trình x + £ 2 + là:
	a) Æ 	b) (–¥; 2)	c) {2}	d) [2; +¥)
x = –3 thuộc tập nghiệm của bất phương trình nào sau đây?
	a) (x+3)(x+2) > 0	b) (x+3)2(x+2)£ 0 	
	c) x+³ 0	d) 
Bất phương trình ³ 0 có tập nghiệm là:
	a) (;2)	b) [; 2]	c) [; 2)	d) (; 2]
Nghiệm của bất phương trình £ 0 là:
	a) (–¥;1)	b) (–3;–1) È [1;+¥)	
	c) [–¥;–3) È (–1;1)	d) (–3;1)
Tập nghiệm của bất phương trình x(x – 6) + 5 – 2x > 10 + x(x – 8) là:
	a) Æ	b) Â	c) (–¥; 5)	d) (5;+¥)
Tập nghiệm của bất phương trình ³ 0 là:
	a) (1;3]	b) (1;2] È [3;+¥)	c) [2;3]	d) (–¥;1) È [2;3]
Nghiệm của bất phương trình là:
	a) (–2; ]	b) (–2;+¥)	
	c) (–2;]È(1;+¥)	d) (–¥;–2) È [;1)
Tập nghiệm của bất phương trình: x2 – 2x + 3 > 0 là:
	a) Æ	b) Â	c) (–¥; –1) È (3;+¥)	d) (–1;3)
Tập nghiệm của bất phương trình: x2 + 9 > 6x là:
	a) Â \ {3}	b) Â	c) (3;+¥)	d) (–¥; 3)
Tập nghiệm của bất phương trình x(x2 – 1) ³ 0 là:
	a) (–¥; –1) È [1; + ¥)	b) [1;0] È [1; + ¥)
	c) (–¥; –1] È [0;1)	d) [–1;1]
Bất phương trình mx> 3 vô nghiệm khi:
	a) m = 0	b) m > 0	c) m < 0	d) m ¹ 0
Nghiệm của bất phương trình là:
	a) x 5	b) x –3 
	c) 5	d) "x
Tìm tập nghiệm của bất phương trình: < 0
	a) Æ	b) {Æ}	c) (0;4)	d) (–¥;0) È (4;+¥)
Tìm m để bất phương trình: m2x + 3 < mx + 4 có nghiệm
	a) m = 1	b) m = 0	c) m = 1 v m = 0	d) "mÎÂ
Điều dấu (X) vào ô đúng hoặc sai của các BPT
	a) 	Đ	S
	b) 	Đ	S
	c) 	Đ	S
Cho bất phương trình: m (x – m) ³ x –1. Các giá trị nào sau đây của m thì tập 	nghiệm của bất phương trình là S = (–¥;m+1]	
	a) m = 1	b) m > 1	b) m < 1	d) m ³ 1
Cho bất phương trình: mx + 6 < 2x + 3m. Các tập nào sau đây là phần bù của 	tập nghiệm của bất phương trình trên với m < 2
	a) S = ( 3; +¥) 	b) S = [ 3, +¥ ) 	c) S = (– ¥; 3);	d) S = (–¥; 3]
Với giá trị nào của m thì bất phương trình: mx + m < 2x vô nghiệm?
	a) m = 0	b) m = 2	c) m = –2	d) m Î R
Bất phương trình: có nghiệm là:
	a) 	b)	
	c) R	d) Vô nghiệm
Tập nghiệm của bất phương trình: là:
	a) Æ	b) R	c) 	d) 	
Cho bất phương rtình : x2 –6 x + 8 ≤ 0 (1). Tập nghiệm của (1) là: 
	a) [2,3]	b) ( – ∞ , 2 ]U[ 4 , + ∞ ) 
	c) [2,8]	d) [1,4]
Cho bất phương trình : x2 –8 x + 7 ≥ 0 . Trong các tập hợp sau đây, tập nào có 	chứa phần tử không phải là nghiệm của bất phương trình.
	a) ( – ∞ , 0 ] 	b) [ 8 , + ∞ ) 	c) ( – ∞ , 1 ] 	d) [ 6 , + ∞ ) 
III. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Tập nghiệm của hệ bất phương trình là:
	a) (1;2)	b) [1;2]	c) (–¥;1)È(2;+¥)	d) Æ
Tập nghiệm của hệ bất phương trình là:
	a) Æ	b) {1}	c) [1;2]	d) [–1;1]
Tập nghiệm của hệ bất phương trình là:
	a) (–¥;1) È (3;+ ¥) 	b) (–¥;1) È (4;+¥) 
	c) (–¥;2) È (3;+ ¥) 	d) (1;4)
Tập nghiệm của hệ bất phương trình là:
	a) (–¥;–3) 	b) (–3;2)	c) (2;+¥)	d) (–3;+¥) 
Hệ bất phương trình có nghiệm khi:
	a) m> 1	b) m =1	c) m< 1	d) m ¹ 1
Hệ bất phương trình có nghiệm khi:
	a) m –2	c) m = 5	d) m > 5
Cho hệ bất phương trình: (1). Tập nghiệm của (1) là:
	a) (–2; ) 	b) [–2; ] 	c) (–2; ] 	d) [–2; )
Với giá trị nào của m thì hệ bất ph.trình sau có nghiệm: 
	a) m > –11	b) m ≥ –11	c) m < –11	d) m ≤ –11
Cho hệ bất ph.trình: (1). Với giá trị nào của m thì (1) vô nghiệm:
	a) m 4 	c) m 4 	d) m 4
Cho hệ bất phương trình: (1). Số nghiệm nguyên của (1) là:
	a) Vô số 	b) 4	c) 8	d) 0 
Hệ bất phương trình : có nghiệm là: 
	a) –1 ≤ x < 2 	b) –3 < x ≤  hay –1 ≤ x ≤ 1 
	c) ≤ x ≤ –1  hay  1 ≤ x < 3 	d) ≤ x ≤ –1  hay x ≥ 1 
Hệ bất phương trình : có nghiệm là: 
	a) –1 ≤ x < 1  hay 	b) –2 ≤ x < 1 
	c) –4 ≤ x ≤ –3  hay –1 ≤ x < 3 	d) –1 ≤ x ≤ 1  hay 
Định m để hệ sau có nghiệm duy nhất:   
	a) m = 1 	b) m = –2 	c) m = 2 	d) Đáp số khác 
Xác định m để với mọi x ta có: –1 ≤ < 7 :
	a) – ≤ m < 1 	b) 1 < m ≤ 	c) m ≤ – 	d) m < 1 
Khi xét dấu biểu thức : f(x) = ta có: 
	a) f(x) > 0 khi (–7 < x < –1 hay 1 < x < 3) 
	b) f(x) > 0 khi (x 3) 
	c) f(x) > 0 khi (–1 1) 
	d) f(x) > 0 khi (x > –1) 
IV. DẤU CỦA TAM THỨC BẬC HAI
Cho tam thức bậc hai: f(x) = x2 – bx + 3. Với giá trị nào của b thì tam thức 	f(x) có hai nghiệm?
	a) b Î [–2; 2]	b) b Î(–2; 2)
	c) b Î (–¥; –2] È [2; +¥ )	d) b Î (–¥; –2) È (2; +¥)
Giá trị nào của m thì phương trình : x2 – mx +1 –3m = 0 có 2 nghiệm trái 	dấu?
	a) m > 	b) m 2	d) m < 2
Gía trị nào của m thì pt: (m–1)x2 – 2(m–2)x + m – 3 = 0 có 2 nghiệm trái dấu?
	a) m 2	c) m > 3	d) 1 < m < 3
Giá trị nào của m thì phương trình sau có hai nghiệm phân biệt?
	(m – 3)x2 + (m + 3)x – (m + 1) = 0 (1)
	a) m Î (–¥;)È(1; +¥) \ {3}	b) m Î (; 1)
	c) m Î (; +¥)	d) m Î Â \ {3}
Tìm m để (m + 1)x2 + mx + m < 0, "xÎÂ ?
	a) m –1	c) m 
Tìm m để f(x) = x2 – 2(2m – 3)x + 4m – 3 > 0, "xÎÂ ?
	a) m > 	b) m > 	c) < m < 	d) 1 < m < 3
Với giá trị nào của a thì bất phương trình: ax2 – x + a ³ 0, "xÎÂ ?
	a) a = 0	b) a < 0	c) 0 < a £ 	d) a ³ 
Với giá trị nào của m thì bất phương trình: x2 – x + m £ 0 vô nghiệm?
	a) m 1	c) m 
Tìm tập xác định của hàm số y = 	
	a) (–¥;]	b) [2;+ ¥)	c) (–¥;]È[2;+¥) d) [; 2]
Với giá trị nào của m thì pt: (m–1)x2 –2(m–2)x + m – 3 = 0 có hai nghiệm x1, 	x2 và x1 + x2 + x1x2 < 1?
	a) 1 2	d) m > 3
Gọi x1, x2 là nghiệm của phương trình: x2 – 5x + 6 = 0 (x1 < x2). Khẳng định 	nào sau đúng?
	a) x1 + x2 = –5	b) x12 + x22 = 37	c) x1x2 = 6	d) = 0
Các giá trị m làm cho biểu thức: x2 + 4x + m – 5 luôn luôn dương là:
	a) m 9	d) m Î Æ
Các giá trị m để tam thức f(x) = x2 – (m + 2)x + 8m + 1 đổi dấu 2 lần là:
	a) m £ 0 Ú m ³ 28	b) m 28	c) 0 < m < 28	d) Đáp số khác.
Tập xác định của hàm số f(x) = là:
	a) 	b) 
	c) 	d) 
Dấu của tam thức bậc 2: f(x) = –x2 + 5x – 6 được xác định như sau:
	a) f(x) 0 với x 3
	b) f(x) 0 với x –2
	c) f(x) > 0 với 2 3
	d) f(x) > 0 với –3 –2
Giá trị của m làm cho phương trình: (m–2)x2 – 2mx + m + 3 = 0 có 2 nghiệm 	dương phân biệt là:
	a) m < 6 Ù m ¹ 2	b) m < 0 v 2 < m < 6	
	c) m > –3 Ù 2 < m < 6	d) Đáp số khác.
Cho f(x) = mx2 –2x –1 . Xác định m để f(x) < 0 với x Î R. 
	a) m  < –1 	b) m < 0 	c) –1 < m < 0 	d) m < 1 và m ≠  0 
Xác định m để phương trình : (m –3)x3 + (4m –5)x2 + (5m + 4)x + 2m + 4 = 0  	có ba nghiệm phân biệt bé hơn 1. 
	a) 3 	b) ( 3) và m ≠  4 
	c) m Î Æ 	d) 0 < m < 
Cho phương trình  : ( m –5 ) x2 + ( m –1 ) x + m = 0   (1). Với giá trị nào của 	m thì (1) có 2 nghiệm x1 , x2  thỏa x1 < 2 < x2   . 
	a) m < 	b) < m < 5 	c) m ≥ 5 	d) ≤ m ≤ 5 
Cho phương trình : x2 – 2x – m = 0  (1). Với giá trị nào của m thì (1) có 2 	nghiệm x1 < x2 < 2 . 
	a) m > 0 	b) m – 
 Cho f(x) = –2x2 + (m –2) x – m + 4 . Tìm m để f(x) không  dương với mọi x. 	a) m Î Æ 	b) m Î R \ {6} 	c) m Î R 	d) m = 6 
Xác định m để phương trình : ( x –1 )[ x2 + 2 ( m + 3 ) x + 4 m + 12 ] = 0  có 	ba nghiệm phân biệt lớn hơn –1. 
	a) m < – 	b) –2 < m < 1 và m ≠  – 
	c) – < m < –1 và m ≠  – 	d) – < m < –3 
Phương trình : (m + 1)x2 – 2(m –1)x + m2 + 4m – 5 = 0  có đúng hai 	nghiệm 	x1 , x2  thoả 2 < x1 < x2 . Hãy chọn kết quả đúng trong các kết quả sau : 
	a) –2 1 	c) –5 < m < –3 	d) –2 < m < 1 
Cho bất phương trình :   ( 2m + 1)x2 + 3(m + 1)x + m + 1 > 0  (1). Với giá trị 	nào của m thì bất phương trình trên vô nghiệm. 
	a) m ≠ 	b) m Î (–5; –1) 	c) m Î [–5; –1] 	d) m Î Æ 
Cho phương trình : mx2 –2 (m + 1)x + m + 5  (1). Với giá trị nào của m thì (1) 	có 2 nghiệm x1, x2  thoả x1 < 0 < x2 < 2 . 
	a) –5 1 	d) m > –1 Ù m ≠ 0 
Cho f(x) = –2x2 + (m + 2)x + m – 4 . Tìm m để f(x) âm với mọi x. 
	a) m Î (–14; 2) 	b) m Î [–14;2]	c) m Î (–2; 14) 	d) m 2 
Tìm m để phương trình : x2 –2 (m + 2)x + m + 2 = 0  có một nghiệm thuộc 	khoảng (1; 2) và nghiệm kia nhỏ hơn 1. 
	a) m = 0 	b) m – c) m > – 	d) 1 < m < – 
Cho f(x) = 3x2 + 2(2m –1)x + m + 4 . Tìm m để f(x) dương với mọi x. 
	a) m b) –1 < m < 	c) –  < m < 1 	d) –1 ≤  m  ≤
Tài liệu đính kèm:
TRON_BO_TRAC_NGHIEM_KHOI_10HAY.doc