Bài giảng Hình học Lớp 10 - Chương II - Bài1: Giá trị lượng giác của một góc bất kỳ (từ 0⁰ đến 180⁰)

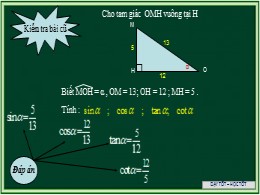
DẠY TỐT – HỌC TỐT 
Kiểm tra bài cũ 
Cho tam giác OMH vuông tại H 
H 
M 
O 
5 
13 
12 
α 
Biết MOH = α , OM = 13; OH = 12 ; MH = 5 . 
Tính : 
Đáp án 
DẠY TỐT – HỌC TỐT 
Chương II : TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG 
Bài 1 : GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KỲ 
( từ 0 0 đến 180 0 ) 
1 . Định nghĩa 
*) Nửa đường tròn đơn vị 
O 
x 
y 
1 
1 
- 1 
*) Nửa đường tròn được gắn vào hệ trục Oxy, 
 c ó tâm trùng với gốc O, 
c ó bán kính bằng 1, 
 phía trên trục hoành 
M 
x 
y 
y 0 
x 0 
O 
A 
*) Giá trị lượng giác của góc là 
DẠY TỐT – HỌC TỐT 
2 . Tính chất 
?1 Tính và so sánh 
 Tính và so sánh 
 Tính và so sánh 
 Tính và so sánh 
Bài làm 
Ta có: 
v à 
Vậy 
Ta có: 
v à 
Vậy 
Ta có: 
v à 
Vậy 
Ta có: 
v à 
Vậy 
*) Công thức lượng giác giữa hai góc bù nhau 
sin(180 0 - ) = sin 
cos(180 0 - ) = cos 
tan(180 0 - ) = tan , ≠ 90 0 
cot(180 0 - ) = cot , 0 0 <  < 180 0 
Ví dụ 1: 
Cho 
Ta có: 
DẠY TỐT – HỌC TỐT 
3 . G iá trị lượng giác của các góc đặc biệt 
GTLG 
0 0 
30 0 
45 0 
60 0 
90 0 
120 0 
135 0 
150 0 
180 0 
0 
1 
0 
1 
0 
0 
0 
-1 
0 
1 
1 
-1 
-1 
DẠY TỐT – HỌC TỐT 
4. Góc của hai vectơ 
O 
A 
B 
Cho hai vect ơ và đều khác . Từ điểm O bất kì vẽ và . Góc với số đo từ đến được gọi là góc giữa hai vectơ và . 
Kí hiệu . 
Nếu thì ta nói và vuông góc nhau. Kí hiệu hoặc . 
a) Định nghĩa 
 +) Từ định nghĩa ta có 
 +) Góc giữa hai vectơ cùng hướng bằng 
b) Chú ý 
DẠY TỐT – HỌC TỐT 
Ví dụ 2: Cho tam giác ABC vuông tại A và có Khi đó: 
DẠY TỐT – HỌC TỐT 
5 . Sử dụng máy tính bỏ túi để tìm giá trị lượng giác của một góc 
*) Chuyển máy tính về chế độ Deg 
*) Tính: 
Bấm máy sin 63 ’ ’’ 52 ’ ’’ 41 ’ ’’ = 
*) Tìm x biết sin x = 0,3502 
Bấm máy = 0’ ’’ 
*) Các giá trị lượng giác cos và tan được tính tương tự 
 HƯỚNG DẪN TIẾT SAU 
*) Học thuộc định nghĩa GTLG; C ông thức lượng giác của hai góc bù nhau 
*) Học thuộc các giá trị lượng giác của các góc có số đo đặc biệt 
*) Học thuộc định nghĩa và cách tìm góc giữa hai vectơ 
*) G iải BT1, BT2, BT5, BT6 / SGK Trang 40