Chủ đề: Bất phương trình và hệ bất phương trình mọt ẩn

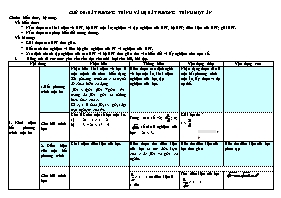
CHỦ ĐỀ: BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH MỌT ẨN
Chuẩn kiến thức, kỹ năng.
Về kiến thức: 
Nắm được các khái niệm về BPT, hệ BPT một ẩn; nghiệm và tập nghiệm của BPT, hệ BPT; điều kiện của BPT; giải BPT.
Nắm được các phép biến đổi tương đương.
Về kĩ năng:
Giải được các BPT đơn giản.
Biết cách tìm nghiệm và liên hệ giữa nghiệm của PT và nghiệm của BPT.
Xác định nhanh tập nghiệm của các BPT và hệ BPT đơn giản dưa vào biến đổi và lấy nghiệm trên trục số.
Bảng mô tả các mức yêu cầu cần đạt cho mỗi loại câu hỏi, bài tập.	
Nội dung
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
I. Khái niệm bất phương trình một ẩn
1.Bất phương trình một ẩn
Nhận biết khái niệm về bpt là một mệnh đề chứa biến dạng Bất phương trình ẩn x là mệnh đề chứa biến có dạng:
 f(x) < (g(x) (f(x) £ g(x)) (*)
trong đó f(x), g(x) là những biểu thức của x.
Số x0 Î R thoả f(x0) < g(x0) đgl một nghiệm của (*).
Hiểu được các định nghĩa về bpt một ẩn, khái niệm nghiệm của bpt, tập nghiệm của bpt.
Nhận dạng được đâu là một bất phương trình một ẩn, lấy được ví dụ cụ thể.
Câu hỏi minh họa
Cho HS nêu một số bpt một ẩn. 
a)	2x + 1 > x + 2
b) 	3 – 2x £ x2 + 4
Trong các số –2; ; p; , số nào là nghiệm của bpt:	2x £ 3.
Giải bpt đó ?
x £ 	 
2. Điều kiện của một bất phương trình 
Khái niệm điều kiện của bpt.
Hiểu được tìm điều kiện của bpt là tìm điều kiện của x để f(x) và g(x) có nghĩa.
Biết tìm điều kiện của bpt đơn gián
Biết tìm điều kiện của bpt phức tạp
Câu hỏi minh họa
 > x + 1 có điều kiện là x0
Tìm điều kiện của bpt > x + 1
3. Bất phương trình chứa tham số
Nắm khái niệm về bpt chứa tham số
Lấy được ví dụ về bpt chứa tham số 
2x – m > 0 (tham số m)
Biết được nghiệm của bpt phụ thuộc vào tham số.
Biện luận nghiệm của bpt theo tham số
II. Hệ BPT một ẩn
2.1 Định nghĩa
Nhận biết khái niệm hệ bpt mộ ẩn.Hệ bpt ẩn x gồm một số bpt ẩn x mà ta phải tìm các nghiệm chung của chúng.
Lấy được một ví dụ về hệ bpt một ẩn
Biết cách giải được hệ bpt bằng cách giải từng bpt rồi kết hợp nghiệm của hệ bpt để đưa ra tập nghiệm của bpt.
Cho ví dụ rồi giải được một hệ bpt đơn giản. Đưa ra tập nghiệm của hệ đã đưa ra.
Câu hỏi minh họa
VD2.	
a) 3x + 2 > 5 – x
b) 2x + 2 £ 5 – x
S1 = 
b) S2 = (–¥; 1]
S = S1 Ç S2 = 
III. Một số phép biến đổi bpt 
1. BPT tương đương
Nhận biết khái niệm hai bpt tương đương:
Hai bpt (hệ bpt) có cùng tập nghiệm đgl hai bpt (hệ bpt) tương đương.
Hiểu được khái niệm
Nhận biết được hai bpt bất kỳ có tương đương hay không.
VD. a) 3 – x ³ 0	b) x + 1 ³ 0 
2. Phép biến đổi tương đương
Để giải một bpt hay hệ bpt ) ta biến đổi nó thành những bpt (hệ bpt) tương đương cho đến khi được bpt (hệ bpt) đơn giản mà ta có thể viết ngay tập nghiệm. 
Một số phép biến đổi tương đương thông thường: 
a) Cộng (trừ): Cộng (trừ) hai vế của bpt với cùng một biểu thức mà không làm thay đổi điều kiện của bpt ta được một bpt tương đương.
b) Nhân (chia): Nhân (chia) hai vế của bpt với cùng một biểu thức luôn nhận giá trị dương (mà không làm thay đổi điều kiện của bpt
· Nhân (chia) hai vế của bpt với cùng một biểu thức luôn nhận giá trị âm (mà không làm thay đổi điều kiện của bpt) và đổi chiều bpt ta được một bpt tương đương.
c) Bình phương: Bình phương hai vế của một bpt có hai vế không âm mà không làm thay đổi điều kiện của nó ta được một bpt tương đương
Biết áp dụng các phép biến đổi thông thương để giải một số bpt đơn giản:
Biết áp dụng các phép biến đổi thông thương để giải một số bpt phức tạp hơn
Câu hỏi minh họa
Hệ bpt: tương đương với hệ bpt nào sau đây:
a) 	b) 
c) 	d) 
VD. Giải hệ bpt
 Û 
	Û –1 £ x £ 1
Giải bpt sau và nhận xét các phép biến đổi ?
Û x > 
Năng lực hướng tới.
Năng lực chủ yếu:
Năng lực tư duy (tư duy nhìn nhận hai bpt như thế nào là tương đương và biết cách biến đổi các bpt tương đương).
Năng lực cần hình thành, phát triển:
Năng lực tự học.
Năng lực giải quyết vấn đề trong việc tìm lời giải một bpt.
Phương pháp dạy học:
Phương pháp trực quan.
Nêu vấn đề, giải quyết vấn đề kết hợp đàm thoại gợi mở.