Chuyên đề Phương trình và bất phương trình chứa căn thức
* Phương pháp 5 : Nhẩm nghiệm và sử dụng tính đơn điệu để chứng minh nghiệm duy nhất
* Ta thường sử dụng các tính chất sau:
· Tính chất 1: Nếu hàm số f tăng ( hoặc giảm ) trong khỏang (a;b) thì phương trình f(x) = C có không quá một nghiệm trong khỏang (a;b).
( do đó nếu tồn tại x0 (a;b) sao cho f(x0) = C thì đó là nghiệm duy nhất của phương
trình f(x) = C)
Bạn đang xem tài liệu "Chuyên đề Phương trình và bất phương trình chứa căn thức", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
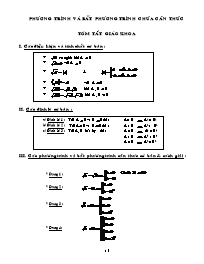
PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH CHỨA CĂN THỨC TÓM TẮT GIÁO KHOA I. Các điều kiện và tính chất cơ bản : * có nghĩa khi A 0 * với A 0 * & * với A 0 * khi A , B 0 * khi A , B 0 II. Các định lý cơ bản : a) Định lý 1 : Với A 0 và B 0 thì : A = B A2 = B2 b) Định lý 2 : Với A 0 và B 0 thì : A > B A2 > B2 c) Định lý 3 : Với A, B bất kỳ thì : A = B A3 = B3 A > B A3 > B3 A = B A2 = B2 III. Các phương trình và bất phương trình căn thức cơ bản & cách giải : * Dạng 1 : * Dạng 2 : * Dạng 3 : * Dạng 4: IV. Các cách giải phương trình căn thức thường sử dụng : * Phương pháp 1 : Biến đổi về dạng cơ bản Ví dụ : Giải phương trình sau : 1) (x=6) 2) Bài tập rèn luyện: 1) () 2) () 3) ( 4) () * Phương pháp 2 : Đặt điều kiện (nếu có) và nâng luỹ thừa để khử căn thức Ví dụ : Giải phương trình sau : 1) ( 2) (x=2) Bài tập rèn luyện: 1) () 2) () 3) () 4) () * Phương pháp 3 : Đặt ẩn phụ chuyển về phương trình hoặc hệ pt đại số Ví dụ : Giải các phương trình sau : 1) 2) 3) 4) Bài tập rèn luyện: 1) () 2) (x=5) 4) 5) * Phương pháp 4 : Biến đổi phương trình về dạng tích số : A.B = 0 hoặc A.B.C = 0 Ví dụ : Giải phương trình sau : * Phương pháp 5 : Nhẩm nghiệm và sử dụng tính đơn điệu để chứng minh nghiệm duy nhất * Ta thường sử dụng các tính chất sau: Tính chất 1: Nếu hàm số f tăng ( hoặc giảm ) trong khỏang (a;b) thì phương trình f(x) = C có không quá một nghiệm trong khỏang (a;b). ( do đó nếu tồn tại x0 (a;b) sao cho f(x0) = C thì đó là nghiệm duy nhất của phương trình f(x) = C) Tính chất 2 : Nếu hàm f tăng trong khỏang (a;b) và hàm g là một hàm giảm trong khỏang (a;b) thì phương trình f(x) = g(x) có nhiều nhất một nghiệm trong khỏang (a;b) . ( do đó nếu tồn tại x0 (a;b) sao cho f(x0) = g(x0) thì đó là nghiệm duy nhất của phương trình f(x) = g(x)) Ví dụ : Giải các phương trình sau : 1) 2) Bài tập rèn luyệnï: 1) (x=3) 2) (x=4) * Phương pháp 6 : Sử dụng bất đẳng thức định giá trị hai vế của phương trình Ví dụ: Giải phương trình V. Các cách giải bất phương trình căn thức thường sử dụng : * Phương pháp 1 : Biến đổi về dạng cơ bản Ví dụ : Giải các bất phương trình sau : 1) 2) 3) 4) Bài tập rèn luyện: 1) () 2) () 3) () 4) () 5) * Phương pháp 2 : Đặt điều kiện (nếu có) và nâng luỹ thừa để khử căn thức Ví dụ : Giải bất phương trình sau : Bài tập rèn luyệnï: 1) () 2) () 3) () * Phương pháp 3 : Đặt ẩn phụ chuyển về bất phương trình đại số Ví dụ : Giải phương trình sau : 1) 2) Bài tập rèn luyệnï: 1) () 2) (-9<x<4) * Phương pháp 4 : Biến đổi phương trình về dạng tích số hoặc thương số Ví dụ : Giải các bất phương trình sau : 1) 2) 3) Bài tập rèn luyệnï: 1) () 2) ()
Tài liệu đính kèm:
 Chuyên đề PT và BPT chứa căn thức.doc
Chuyên đề PT và BPT chứa căn thức.doc





