GIáo án Đại số 10 Bài 3: Hàm số bậc hai

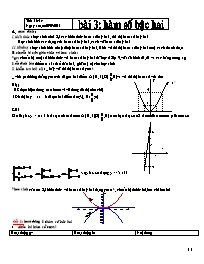
Tiết 13-14
Ngày soạn:20\9\2011
mục đích :
I.kiến thức : học sinh nhớ lại các kiến thức hàm số bậc hai , đố thị hàm số bậc hai
Học sinh biết các dạng của hàm số bậc hai ,cách vẽ hàm số bậc hai
II.kĩ năng : học sinh biết nhận diện hàm số bậc hai. Biết vẻ đồ thị hàm số bậc hai một cách thành thạo
B.chuẩn bị của giáo viên và học sinh :
*gv: chuẩn bị một số kiến thức về hàm số bậc hai đã học ở lớp 9,vẽ sẵn hình 21,21 và các bảng trong sgk 
1.ổn định lớp:kiểm tr sỉ số sổ đầu bài, giữ trật tự cho học sinh
2. kiểm tra bài cũ : _ hãy vẽ đồ thị hàm số y=x2 
4
1
y
y= x2
_ viết pt đường thẳng y=ax+b đi qua hai điểm A(0;3), B(;0)và vẻ đồ thị hàm số vừa tìm
Giải 
+HS thực hiện đúng các bước và vẻ đúng đồ thị cho (4đ)
+Đồ thị hs y = ax + b đi qua hai điểm A(0;3), B(;0)
Giải
Đồ thị hs y = ax + b đi qua hai điểm A(0;3), B(;0) nên tọa độ của 2 điểm thỏa mản pt hàm số vậy hs cĩ dạng y= -5x+3 -2
1
1
3
x
0
H
*học sinh cần ôn lại kiến thừc về hàm số bậc hai dạng y=ax2 , chuẩn bị thước kẻ,bút chì bút kẻ
 tiết 1:hoạt động 1 :hàm số bậc hai
nhắc lại hàm số y=ax2 
Hoạt động gv
Hoạt động hs
Nội dung
shàm số quay bề lõm lên trên khi nào? Quay xuống khi nào?
scó toạ đỉnh như thế nào?
stính đối xứng như thế nào?
+ quay bề lõm lên khi a> 0,xuống dưới khi a<0 
+ đỉnh có toạ độ là góc toạ độ (0;0)
+là hàm số chẵn nên đồ thị nhận trục oy làm trục đối xứng 
I.ĐỒ THỊ CỦA HÀM SỐ BẬC HAI
đồ thị hàm số dạng y=ax2 
_có bề lõm quay lên khi a> 0,quay xuống dưới khi a<0 
_ đỉnh có toạ độ là góc toạ độ (0;0)
_ là hàm số chẵn nên đồ thị nhận trục oy làm trục đối xứng
hoạt động 2: Tìm hiểu quan hệ giữa các đồ thị của các hàm số y = ax2 + bx + c và y = ax2 (a0)
gv hướng dẫn học sinh thực hiện phép biến đổi với 
Hoạt động gv
Hoạt động hs
Nội dung
snếu Thì y như thế nào? 
svậy điểm có vị trí như thế nào đối với đồ thị hs y
Nếu a>0;a<0 thì y như thế nào?
scó nhận xét gì về đỉnh 0(0;0) của hàm số y=ax2 điểm của hàm số y=ax2 +bx+c
+hàm số có dạng 
+điểm thuộc đồ thị hsố 
Nếu a>0 thì do đó I là điểm thấp nhất
Nếu a<0 thì do đó I là điểm cao nhất
+điểm của hàm số 
y=ax2 +bx+c đóng vai trò như đỉnh
0(0;0) của hàm số y=ax2 
b.hàm số y=ax2+bx+c (x0) nhận xét sgk trang 43
chú ý: *a>0 hàm số bậc hai đạt gía trị nhỏ nhất taị x= giá trị nhỏ nhất bằng 
*a<0 hàm số đạt giá trị lớn
nhất tại x= giá trị lớn nhất bằng 
 y= ax2+bx+c 
Hoạt động 2:hàm số bậc hai y=ax2+bx +c 
y
 x
y
O
 x
O
 y= ax2+bx+c 
Đồ thị hàm số y=ax2+bx +c là đồ thị của hàm số y=ax2 qua một phép “dịch chuyển”
Hình 1
 aa>0 a<0 
Hoạt động gv
Hoạt động hs
Nội dung
stừ đồ thị hàm số y= ax2 suy ra đồ thị của hàm số y=x2+bx+c (a0) có toạ độ đỉnh là như thế nào ?
scó trục đối xứng như thế nào?
scho hàm số y=2x2+3x+1 có :
a/ tìm trục đối xứng ?
b / tìm toạ độ đỉnh ?
+ có đỉnh là
I
+có trục đối xứng là x=
+a/hàm số có trục đối xứng là:x= 
b/ có toạ độ đỉnh I() 
2.đồ thị: Hsố y=ax2+bx +c là một đường parabol có đỉnh là điểm 
có trục đối xứng là đường thẳng x= parabol này quay bề lõm lên trên nếu a>0, quay bề lõm xuống dưới nếu a<0
Vd: Bài 1: parabol: y= có toạ độ đỉnh là: (0;1) 
bài 2: với gia trị nào của x thì
 y= x2-5x + 4 <0 
 giải
bài 3: đồ thị hàm số y=(x-2)2 có trục đối xứng là đường thẳng x=2 
Hoạt động 3:* cách vẽ đồ thị hàm số bậc hai y=ax2 +bx +c (a0)
Giáo viên : hướng dẩn học sinh đưa ra các bước vẽ parabol 
B1: xác định hệ số a ,Toạ độ đỉnh I()
B2: Vẽ trục đối xứng x=
B3 :Xđ giao điểm với các trục toạ độ ;Xác định thêm một số điểm thuộc đồ thị , chẳng hạn điểm đối xứng với giao điểm của đồ thị qua trục đối xứng 
B4: Vẽ hình cần chú ý hệ số bề lõm lên trên nếu a>0, quay bề lõm xuống dưới nếu a<0 
Hoạt động 4: Củng cố Vd : vẽ đồ thị các hàm số sau: y= x2-4x +3 ;y= -x2 –3x ;y= -2x2 +x –1 ;y=3x2 +1
Hoạt động gv
Hoạt động hs
Nội dung
Vd: vẻ đồ thị hàm số ta cần các bước như thế nào? Hãy vẽ đồ thị hàm số sau y=2x2- 3x+1
sXác định hệ số a=? và đỉnh của parabol
sXác định trục đối xứng của parabol ? 
sXác định giao điểm của parabol và oy ? Xác định giao điểm của parabol và ox ? 
sXác định đỉnh và bề lõm của parabol trên 
: xác định hệ số a ,Toạ độ đỉnh I()
B2: Vẽ trục đối xứng x=
B3 :Xđ giao điểm với các trục toạ độ ;Xác định thêm một số điểm thuộc đồ thị , chẳng hạn điểm đối xứng với giao điểm của đồ thị qua trục đối xứng 
B4: Vẽ hình cần chú ý hệ số bề lõm lên trên nếu a>0, quay bề lõm xuống dưới nếu a<0
+ a=2>0đỉnh
+Trục đối xứng có phương trình 
+Giao điểm với oy là A(0 ; - 1).Giao điểm của parabol và ox là B(1 ; 0) và 
+Vì a = 3 >0 nên parabol có bề lõm quay lên trên
Vd: vẻ đồ thị hàm sốy=3x2-2x-1
giải: parabol có a=3>0 có bề lõm quay lên trên; đỉnh ,trục đối xứng có giao với trục ox A(0;-1)
giao với trục oy là B(1 ; 0) và ; D
-1
1
2
3
-4
3
1
3
-1
3
0
y
x
Bài tập vẻ đồ thị hàm số 
a) ; b) 
 s Nêu các bứơc vẽ parabol ?
s Tìm đỉnh của parabol
s Trục dối xứng và bảng biến thiên ?
sTìm giao trục hồnh giao trục tung? 
s Giá trị nhỏ nhất của hàm số ?
+B1:ĐỉnhI()
B2:Trục đối xứng x=
B3: Vẽ
+Đỉnh Với 
Vậy 
+Trục đối xứng x = 1
+ Giao trục tung tại (0;-1)
Giao trục hồnh tại () ; (
+Giá trị nhỏ nhất của hàm số là Min 
y = -2 khi x = 1
+Lập bảng biến thiên và vẻ đồ thị hàm số a) 
	Giải 
– Đỉnh Với 
Vậy 
O
y
x
1
-2
x = 1
-1
2
–Trục đối xứng x = 1
– BBT:
–Vẽ :
4. Củng cố :
	_ Nêu các bước vẽ đố thị hàm số bậc hai B1: xác định hệ số a ,Toạ độ đỉnh I()
B2: Vẽ trục đối xứng x=
B3 :Xđ giao điểm với các trục toạ độ ;Xác định thêm một số điểm thuộc đồ thị , chẳng hạn giao điểm của đồ thị với trục hoành ,trục tung
5Dặn dò :bài tập 1_Cho parabol Tìm :	o Đỉnh ? 
	o Trục đối xứng ? 
	o Bề lõm của parabol như thế nào?
2-: cho hàm số y=2x2+3x+1 có :
a/ khảo sát sự biến thiên và vẻ đồ thị hàm số trên
b/ tìm những giá trị nào của x để hàm số có y>0
BÀI HỌC KINH NGHIỆM:.
.
.
Tiết 14
Ngày soạn:20\9\2011
I. MỤC TIÊU:
	Kiến thức: 	
Hiểu quan hệ giữa đồ thị của các hàm số y = ax2 + bx + c và y = ax2.
Hiểu và ghi nhớ các tính chất của hàm số y = ax2 + bx + c.
	Kĩ năng: 
Lập được bảng biến thiên của hàm số bậc hai, xác định toạ độ đỉnh, trục đối xứng, vẽ được đồ thị hàm số bậc hai.
Đọc được đồ thị của hàm số bậc hai, từ đồ thị xác định được: trục đối xứng, các giá trị x để y> 0, y < 0.
Tìm được phương trình của parabol khi biết một trong các hệ số và đồ thị đi qua hai điểm cho trước.
	Thái độ: 
Rèn luyện tính cẩn thận, chính xác khi vẽ đồ thị. Luyện tư duy khái quát, tổng hợp.
II. CHUẨN BỊ:
	Giáo viên: Giáo án. Hình vẽ minh hoạ.
	Học sinh: SGK, vở ghi. Đọc bài trước. 
	Ôn lại kiến thức đã học về hàm số y = ax2. Dụng cụ vẽ đồ thị.
III. HOẠT ĐỘNG DẠY HỌC:
	1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
	2. Kiểm tra bài cũ: 
Câu hỏi:Cho hàm số y = –x2 + 4. Tìm toạ độ đỉnh, trục đối xứng của đồ thị hàm số?
Trả lời: I(0; 4). (D): x = 0.
Giảng bài mới:
Hoạt động 1:chiều biến thiên của hàm số bậc hai
Hoạt động gv
Hoạt động hs
Nội dung
squa hình 1 hãy cho nhận xét về chiều biến thiên của hàm số bậc hai trong khoảng Và trong khoảng 
sHàm số 
Đồng biền và nghịch biến trên khoảng nào?
smuốn vẽ được bảng biến thiên ta cần xác định những dữ kiện gì ?
sNêu sự biến thiên của hàm số ?
snêu lại cách vẻ đồ thị hàm số bậc 2 dạng 
+nếu a>0 hàm số nghịch biến trong khoảng 
và đồng biến trong khoảng 
*nếu a<0 hàm số đồng biến trong khoảng 
và nghịch biến trong khoảng
+Đồng biền và nghịch biến 
+ ta cần tìm hệ số a, và toạ độ đỉnh I
+hsố đồng biến và nghịch biến từ 
+B1: xác định hệ số a ,Toạ độ đỉnh I()
B2: Vẽ trục đối xứng x=
B3 :Xđ giao điểm với các trục toạ độ ;Xác định thêm một số điểm thuộc đồ thị , chẳng hạn điểm đối xứng với giao điểm của đồ thị qua trục đối xứng 
B4: Vẽ hình cần chú ý hệ số bề lõm lên trên nếu a>0, quay bề lõm xuống dưới nếu a<0
II) chiều biến thiên của hàm số bậc hai:
Dựa vào đồ thị hàm số bậc hai ta có bảng biến thiên sau 
a>0
 +
¥
+
¥
-b
2a
-
4a
-
¥
+
¥
y
x
 a<0
-
¥
-
¥
-b
2a
-
4a
-
¥
+
¥
y
x
vd xét sự biến thiên của hàm số sau và vẻ đồ thị hàm số sau y=-x2- 3x
ta có a=-1<0 ,toạ độ đỉnh
I -
¥
-
¥
9
4
-3
2
-
¥
+
¥
y
x
 hsố đồng biến và nghịch biến từ 
 Đồ thị hsố là một (p) có bề lõm quay xuống và đi qua các điểm 
A(0;0);B(-3;0);C(-2;2);D(-1;2)
1
1
9
4
-3
2
-1
2
-2
-3
0
y
x
Hoạt động 2: Luyện tập xác định chiều biến thiên của hàm số bậc hai
· Cho mỗi nhóm xét chiều biến thiên của một hàm số.
s Để xác định chiều biến thiên của hàm số bậc hai, ta dựa vào các yếu tố nào?
· Các nhóm thực hiện yêu cầu
+Hệ số a và toạ độ đỉnh
Đồng biến
Nghịch biến
a
(–¥; –1)
(–1; +¥)
b
(0; +¥)
(–¥; 0)
c
(–¥; 2)
(2; +¥)
d
(1; +¥)
(–¥; 1)
Ví dụ:
Xác định chiều biến thiên của hàm số: 
a) y = –x2 – 2x + 3
b) y = x2 + 1
c) y = –2x2 + 4x – 3
d) y = x2 – 2x
Hoạt động 3: Luyện tập khảo sát hàm số bậc hai
Bài tập khảo sát và vẻ đồ thị hàm số ; y = –x2 + 4x – 3
s Nêu các bứơc vẽ parabol 
– Tìm tập xác định
– Tìm toạ độ đỉnh
– Xác định chiều biến thiên
– Xác định trục đối xứng
– Tìm toạ độ giao điểm của đồ thị với các trục toạ độ.
– Vẽ đồ thị
– Dựa vào đồ thị, xác định x để y 0
s Tìm đỉnh của parabol
s Trục dối xứng và bảng biến thiên ?
sTìm giao trục hồnh giao trục tung? 
s Giá trị nhỏ nhất của hàm số ?
+B1:ĐỉnhI()
B2:Trục đối xứng x=
B3: Vẽ
+Đỉnh Với 
Vậy 
+Trục đối xứng x = 0
+ Giao trục tung tại (0;1)
Khơng cĩ giao trục hồnh 
+Giá trị nhỏ nhất của hàm số là Min 
y = 1 khi x = 0
+Lập bảng biến thiên và vẻ đồ thị hàm số a) 
	Giải 
– Đỉnh Với 
Vậy 
–Trục đối xứng x = 0
– BBT:
-
¥
-
+¥
-
¥
+
¥
y
x
0
1
–Vẽ :
1
1
3
x
0
sKhảo sát hàm số và vẽ đồ thị hàm số
 – Tìm tập xác định
– Tìm toạ độ đỉnh
– Xác định chiều biến thiên
– Xác định trục đối xứng
– Tìm toạ độ giao điểm của đồ thị với các trục toạ độ.
– Vẽ đồ thị
· hs vẻ hình:- 
–Trục đối xứng x = 2
– BBT:a< bề lõm quay xuống
-
¥
-
-¥
-
¥
+
¥
y
x
2
1
–Vẽ :đồ thị hàm số đi qua các điểm
(0;-3);(1;0);(3;0)
Khảo sát hàm số và vẽ đồ thị hàm 
y = –x2 + 4x – 3
giải
Đỉnh Với 
Vậy 
–Trục đối xứng x = 2
– BBT:
-
¥
-
-¥
-
¥
+
¥
y
x
2
1
–Vẽ :đồ thị hàm số đi qua các điểm
(0;-3);(1;0);(3;0)
4. Củng cố :	_ Nêu các bước vẽ đố thị hàm số bậc hai : B1: xác định hệ số a ,Toạ độ đỉnh I()
B2: Vẽ trục đối xứng x=
B3 :Xđ giao điểm với các trục toạ độ ;Xác định thêm một số điểm thuộc đồ thị , chẳng hạn điểm đối xứng với giao điểm của đồ thị qua trục đối xứng 
B4: Vẽ hình cần chú ý hệ số bề lõm lên trên nếu a>0, quay bề lõm xuống dưới nếu a<0 	_
Bài tập :Cho parabol khảo sát và vẻ đồ thị hàm số.tìm m để y>0?
-1
-1
3
-2
0
y
x
5. Dặn dò :_Học thuộc cách vẽ parabol
	_Làm bài tập 1;2;3;4sách giáo khoa trang 49
bài tập 
1/ hàm số khảo sát và vẻ đồ thị hàm số trên
 2/viềt pt của parabol y=ax2 +bx+c ứng với hình sau
BÀI HỌC KINH NGHIỆM .