Giáo án Hình cơ bản 10 - Chương II - Bài 1: Hệ thức lượng trong tam giác

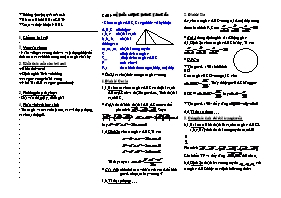
* Trường THPT Nguyễn Hữu Huân
* Giáo án Hình 10 Ban KHTN
* Soạn và thực hiện: NHHL
1. Kiểm tra bài cũ:
- 
2. Yêu cầu chung: 
- Nắm vững các công thức và vận dụng được để tính toán các chi tiết trong một tam giác bất kỳ
3. Kiến thức nền cho bài mới
+ Biến đổi vectơ
+ Định nghĩa Tích vô hướng
+ các góc cùng chắn 1 cung 
+ Nhớ Tỉ số LG các góc quen thuộc
3. Phương pháp dạy học:
- Đặt vấn đề, gợi ý, diễn giải
4. Phần việc của học sinh:
- Tham gia vào các nhận xét, các ví dụ áp dụng, các hoạt động D
- 
- 
- 
-
- 
- 
- 
- 
-
-
- 
- 
- 
C2B1– HỆ THỨC LƯỢNG TRONG TAM GIÁC 
§ Cho tam giác ABC. Các qui ước về ký hiệu:
A, B, C	: đỉnh/góc
a, b, c	: độ dài cạnh
ha, hb, hc	: độ dài đường cao
ma, mb, mc	: độ dài trung tuyến
S	: diện tích tam giác 
SABC	: diện tích tam giác ABC
P	: nủa chu vi
R, r	: bán kính đtròn ngoại tiếp, nội tiếp 
w Ôn lại các hệ thức trong tam giác vuông 
1. Định lý Cosin
1.1. Bài toán: cho tam giác ABC có độ dài cạnh AB=c, AC=b và độ lớn góc A=a. Tính độ dài cạnh BC.
w Gợi ý: do đã biết độ dài AB, AC nên có thể phân tích . Suy ra
= 
hay 
1.2. Định lý: cho tam giác ABC. Ta có:
Từ đây suy ra: 
w Câu hỏi: nhìn thế nào về dấu của cosA để biết góc A nhọn, tù hay vuông ?
1.3. Ví dụ áp dụng: . . . 
2. Định lý Sin
D4. cho tam giác ABC vuông tại A nội tiếp trong đtròn bán kính R. Cmr: 
w Gợi ý: dùng định nghĩa tỉ số lượng giác
2.1. Định lý: cho tam giác ABC bất kỳ. Ta có:
w HD Cm: 
* T.h: góc A < 900: kẻ đkính BD
Có tam giác BCD vuông tại C cho . Thấy được góc BAC bằng góc BDC Þ hay 
* T.h: góc A >900: để ý rằng 
2.2. Ví dụ áp dụng. . . . 
3. Công thức tính độ dài trung tuyến
3.1. Bài toán: Biết độ dài 3 cạnh tam giác ABC là a,b,c. Hãy tính đô dài trung tuyến ma=AM
Phân tích 
Khai triển VP và để ý rằng đối nhau.
3.2. Định lý: độ dài các trung tuyến của tam giác ABC được xác định bởi công thức:
3.3. Ví dụ áp dụng . . . 
4. Các công thức tính Diện tích
w nhắc lại công thức đã biết: 
DT tam giác = ½ Đáy . Cao = ½ a.ha (1)
4.1. Định lý: Diện tích tam giác ABC được tính theo một trong các công thức sau:
w HD Cm: 
Từ công thức (1), thay ha bằng bsinC sẽ có công thức (2)
Từ 
4. 2. Ví dụ áp dụng
5. Giải tam giác – Ứng dụng thực tế
* Nội dung tuỳ chọn:
- Để xây dựng công thức tính độ dài trung tuyến, nếu đi theo hướng sau đây được không ?
Phân tích 
- 
- 
* Bài tập về nhà
- 
- 
- 
- 
* Nhận xét, rút kinh nghiệm sau khi thực hiện giáo án
- 
- 
- 
-