Luyện đề thi Học sinh giỏi Toán Hình học Lớp 10
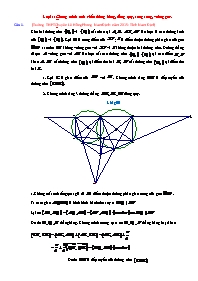
Cho hai đường tròn và cắt nhau tại . lần lượt là các đường kính của và . Gọi là trung điểm của ; là điểm thuộc đường phân giác của góc sao cho không vuông góc với và không thuộc hai đường tròn. Đường thẳng đi qua vuông góc với lần lượt cắt các đường tròn , tại các điểm khác . cắt đường tròn tại điểm thứ hai , cắt đường tròn tại điểm thứ hai .
1. Gọi là giao điểm của với . Chứng minh rằng là tiếp tuyến của đường tròn .
2. Chứng minh rằng 3 đường thẳng đồng quy.
Bạn đang xem 20 trang mẫu của tài liệu "Luyện đề thi Học sinh giỏi Toán Hình học Lớp 10", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Loại 1: Chứng minh tính chất: thẳng hàng, đồng quy, song song, vuông góc. [Trường THPT Chuyên Lê Hồng Phong Nam Định- năm 2015- Tỉnh Nam Định] Cho hai đường tròn và cắt nhau tại . lần lượt là các đường kính của và . Gọi là trung điểm của ; là điểm thuộc đường phân giác của góc sao cho không vuông góc với và không thuộc hai đường tròn. Đường thẳng đi qua vuông góc với lần lượt cắt các đường tròn , tại các điểm khác . cắt đường tròn tại điểm thứ hai , cắt đường tròn tại điểm thứ hai . 1. Gọi là giao điểm của với . Chứng minh rằng là tiếp tuyến của đường tròn . 2. Chứng minh rằng 3 đường thẳng đồng quy. Lời giải 1. Không mất tính tổng quát giả sử là điểm thuộc đường phân giác trong của góc . Ta có tứ giác là hình bình hành nên suy ra Lại có Do đó thẳng hàng. Chứng minh tương tự ta có thẳng hàng Mặt khác Do đó là tiếp tuyến của đường tròn 2. Ta có nên 4 điểm cùng thuộc đường tròn đường kính . Mà nên suy ra là tiếp tuyến của đường tròn đường kính . Do đó (1) Mặt khác (2) Từ (1) và (2) suy ra Vậy 4 điểm cùng thuộc một đường tròn. Gọi là giao điểm của và Vì 4 điểm cùng thuộc một đường tròn nên ta có (3) Ta có (4) Gọi là giao điểm của với Chứng minh tương tự câu 1) ta có là tiếp tuyến của đường tròn Mặt khác tứ giác là hình thang vuông tại và là trung điểm của nên suy ra . Do đó (5) Từ (3), (4), (5) suy ra cùng thuộc trục đẳng phương của hai đường tròn nên thẳng hàng. Vậy 3 đường thẳng đồng quy tại *) Chú ý: Nếu HS không sử dụng góc định hướng thì phải xét các trường hợp vị trí của điểm ( nằm ngoài các đoạn và nằm trong các đoạn ) [Trường THPT Lương Văn Tụy- Ninh Bình- Vòng 2] Cho tam giác nhọn có trực tâm ., là trung điểm của . Các đường phân giác của góc , cắt nhau tại . Chứng minh: a, Góc là góc vuông b, thẳng hàng. [SỞ Bình Định- năm học 2012-2013] Trong tam giác , là chân đường vuông góc hạ từ xuống đường phân giác trong của góc lần lượt là chân đường vuông góc hạ từ các đỉnh xuống đường phân giác trong của góc . Gọi là giao điểm của các đường thẳng và , là giao điểm của các đường thẳng và , là giao điểm của các đường thẳng và . Chứng minh rằng . [Trường THPT Chuyên Hoàng Văn Thụ - năm 2015- Tỉnh Hòa Bình] Cho và hai đường tròn tiếp xúc ngoài với nhau và tiếp xúc trong với . Gọi là tiếp điểm của và ; là tiếp điểm của với . Tiếp tuyến chung tại của cắt tại A. cắt tại ; cắt tại . Chứng minh rằng . cắt ở ; cắt tại . Chứng minh rằng là tâm đường tròn nội tiếp của tam giác . Chứng minh rằng đồng quy. Lời giải a) thuộc trục đẳng phương của và nên suy ra là tứ giác nội tiếp dẫn đến b) Gọi là giao điểm của với . Tam giác vuông tại có là đường cao là tứ giác nội tiếp Suy ra A là tâm đường tròn ngoại tiếp tam giác Dẫn đến Suy ra là phân giác của Rõ ràng là phân giác của (do ) Vì thế là tâm đường tròn nội tiếp tam giác c)Giả sử cắt tại , gọi là bán kính của , . Rõ ràng là tâm vị tự ngoài của và ,lại có Suy ra Dẫn đến thẳng hàng (Menelauyt đảo) Vậy đồng quy. [ ĐỀ THI CHỌN HỌC SINH GIỎI TRẠI HÈ HÙNG VƯƠNG LẦN THỨ XI- CHUYÊN HẠ LONG] Cho hai đường tròn và với cắt nhau tại hai điểm phân biệt . Một đường thẳng d tiếp xúc với đường tròn và lần lượt tại và . Gọi và lần lượt là chân đường vuông góc hạ từ và xuống .Các đường thẳngvà cắt các đường tròn tại và.Chứng minh rằng thẳng hàng. Hướng dẫn giải Gọi là giao điểm của và , khi đó là tâm vị tự ngoài của hai đường tròn và . Đặt , khi đó ta có: Gọi là giao điểm của với và . Khi đó ta có: Mà// // nên Suy ra là trung trực của . Mà là trung trực của . Vậy tứ giác là hình thoi Do đó// hay// . Giả sử biến thành khi đó// Mà thuộc suy ra thuộc do đó . Vậy biến thành . Tương tự ta có biến thành . Suy ra thẳng hàng. Cho đường tròn nội tiếp tiếp xúc với các cạnh tương ứng tại . Đường thẳng cắt tại . Đường tròn đường kính cắt tại (). Gọi () tương ứng là giao của với . Hai đường thẳng và cắt nhau tại . Đường tròn cắt tại và đường tròn cắt tại . Chứng minh rằng đồng quy. Hướng dẫn giải Gọi là trung điểm đoạn . Ta có , do đó điều này suy ra là tiếp tuyến. Do đó . Mặt khác là tiếp tuyến của , do đó cũng là tiếp tuyến của . Vì vậy Suy ra đi qua trung điểm của đoạn ( bổ đề quen thuộc trong hình thang ). Từ đây suy ra là 3 đường trung tuyến của , suy ra ĐPCM. [KỲ THI CHỌN HỌC SINH GIỎI KHU VỰC DUYÊN HẢI VÀ ĐỒNG BẰNG BẮC BỘ NĂM HỌC 2016 - 2017 ] Cho tam giác có . Đường tròn nội tiếp tiếp xúc với và tạitương ứng. Gọi là trung điểm của và là điểm đối xứng với qua . Đường thẳng vuông góc với tại cắt tại là giao điểm thứ hai của với . Chứng minh rằng . [ĐỀ XUẤT ĐỀ THI DUYÊN HẢI BẮC BỘ.Trường THPT Chuyên Hoàng Văn Thụ - Tỉnh Hòa Bình. Năm học 2012-2013] Cho tam giác . Các phân giác ngoài của các góc lần lượt cắt cạnh đối diện tại của tam giác tại . CMR thẳng hàng và thuộc đường thẳng vuông góc với ở đây lần lượt là tâm đường tròn ngoại tiếp và nội tiếp của tam giác Hướng dẫn giải Qua kẻ các đường thẳng vuông góc lần lượt cắt . Có chung trục đt của và là tâm đường tròn bàng tiếp của thẳng hàng. C thẳng hàng và [Đề xuất lớp 11 Sở GD- ĐT Quảng Ninh- Trường THPT Chuyên Hạ Long] Giả sử đường tròn nội tiếp tam giác tiếp xúc với các cạnh theo thứ tự . Đường thẳng qua và song song với cắt tại . Gọi là trung điểm của . Chứng minh rằng: . Hướng dẫn giải Gọi là giao điểm của và . QuaN kẻ đường thẳng // cắt , theo thứ tự từ . Vì hai tứ giácvà nội tiếp nên Mặt khác . Do đó cân tại . Vậy là trung điểm của thẳng hàng. Lại có là trực tâm Gọi là giao điểm của và là giao điểm của và Mà nội tiếp nên(Đpcm). [ĐỀ NGHỊ THI CHỌN HSG VÙNG DUYÊN HẢI BẮC BỘ LỚP 11 - Trêng T.H.P.T Chuyªn Th¸i B×nh.N¨m häc 2013-2014 ] Cho tam giác vuông tại . Hình chữ nhật thay đổi sao cho thuộc , thuộc và thuộc .Chứng minh rằng. 1) 2) luôn đi qua một điểm cố định. Hướng dẫn giải 1) Lấy theo thứ tự thuộc sao cho (h.1). (h.2.1) Ta có: Do đó các tam giác đồng dạng. Vậy 2) Đặt (h.2.2). Theo định lí Pappus: thẳng hàng . Gọi là hình chiếu của trên ; theo thứ tự là trung điểm của , . Dễ thấy thẳng hàng; thẳng hàng; . Vậy Do đó thẳng hàng. Từ và suy ra đi qua (đpcm). (h.2.2) [ ĐỀ THI ĐỀ XUẤT TRẠI HÈ HÙNG VƯƠNG LẦN THỨ XI-TRƯỜNG THPT CHUYÊN TUYÊN QUANG ] Cho tam giác với . Các đường trung tuyến và phân giác trong góc cắt tại và tương ứng. Đường thẳng qua vuông góc với cắt lần lượt tại và ; đường thẳng qua vuông góc với cắt đường thẳng tại . Chứng minh vuông góc với . Hướng dẫn giải Gọi là giao điểm thứ hai của với đường tròn ngoại tiếp tam giác , dễ thấy suy ra vuông góc với .Đặt và xét phép vị tự . Khi đó thuộc , thuộc và hai tam giác và có các cạnh tương ứng song song. Gọi là giao điểm của với , ta có suy ra tứ giác nội tiếp. Từ đó Như vậy nên K là trung điểm, hay thuộc , suy ra trùng . Do song song với mà vuông góc với nên vuông góc với . [TRẠI HÈ HÙNG VƯƠNG-ĐỀ THI CHỌN HỌC SINH GIỎI năm 2015.LẦN THỨ XI ] Cho tam giác có ba góc nhọn, và nội tiếp đường tròn Các đường cao cắt nhau tại Đường thẳng cắt tại Lấy điểm trên sao cho Đường tròn ngoại tiếp tam giác cắt tại Chứng minh rằng a) Ba điểm thẳng hàng. b) Đường thẳng vuông góc với đường thẳng [ Đề 59- TRƯỜNG THPT CHUYÊN VĨNH PHÚC-ĐỀ THI CHỌN HỌC SINH GIỎI VÙNG DUYÊN HẢI VÀ ĐỒNG BẰNG BẮC BỘ LẦN THỨ VIII- NĂM 2015.MÔN TOÁN - LỚP 11 ] Cho tam giác nhọn không cân, nội tiếp đường tròn . là điểm nằm trong tam giác sao cho . Đường tròn đường kính cắt các cạnh lần lượt tại và cắt đường tròn tại điểm khác . Chứng minh rằng đồng quy. Hướng dẫn giải Gọi là đường kính của , dễ thấy thẳng hàng và . Giả sử cắt tại cắt tại . Theo định lý Desargues để chứng minh (hay ) đồng quy ta chỉ cần chứng minh thẳng hàng. Áp dụng định lý Menelaus ta được: Dễ thấy tứ giác EFBC nội tiếp nên Cũng từ nội tiếp suy ra Tứ giác là hình bình hành suy ra . Suy ra . Ta có Thay vào ta được . Từ đó áp dụng định lý menelaus cho tam giác ta suy ra thẳng hàng. Bài toán được chứng minh. [ SỞ GIÁO DỤC VÀ ĐÀO TẠO LÂM ĐỒNG- Trường THPT Chuyên BảoLộc-KỲ THI HSG KHU VỰC DH VÀ ĐBBB LẦN THỨ 9ĐỀ THI ĐỀ NGHỊ MÔN: TOÁN; LỚP: 11] Cho tứ giác nội tiếp có các cặp cạnh đối không song song. Các đường thẳng và cắt nhau tại điểm và các đường chéo và cắt nhau tại . Đường tròn ngoại tiếp các tam giác cắt nhau tại điểm thứ hai . Chứng minh rằng hai đường thẳng và vuông góc. Hướng dẫn giải § Gọi là giao điểm của và, là tâm đường tròn ngoại tiếp tứ giác . Ta dùng kí hiệu tương ứng để chỉ đường tròn ngoại tiếp của tam giác , tứ giác . Ta có lần lượt là trục đẳng phương của các cặp đường tròn và và và nên đồng quy tại hay thẳng hàng. § Không mất tổng quát ta giả sử F nằm giữa và . Ta có (ta có thể dùng góc định hướng cho mọi trường hợp). Suy ra các điểm cùng thuộc một đường tròn ta gọi là . § Tương tự, các điểm cùng thuộc một đường tròn ta gọi là . Ta có lần lượt là trục đẳng phương của các cặp đường tròn và , , và nên đồng quy tại hay thẳng hàng. § Xét cực và đối cực đối với đường tròn, ta có là đối cực của nên vuông góc với Mà thẳng hàng; thẳng hàng nên và vuông góc (điều phải chứng minh). [KỲ THI HỌC SINH GIỎI CÁC TRƯỜNG THPT CHUYÊN KHU VỰC DUYÊN HẢI VÀ ĐỒNG BẰNG BẮC BỘ LẦN THỨ IX, NĂM HỌC 2015 –2016. ĐỀ THI MÔN TOÁN – KHỐI 11 ] Cho tam giác nội tiếp đường tròn. Tiếp tuyến của tại cắt nhau tại . Gọi là đường thẳng chứa phân giác trong góc của tam giác . Các đường trung trực của các đoạn thẳng cắt lần lượt tại và . Gọi là giao điểm của và , là tâm đường tròn nội tiếp tam giác , là trực tâm của tam giác . a. Chứng minh ,đối xứng với nhau qua . b. Chứng minh thẳng hàng. Hướng dẫn giải a) Chứng minh là trung trực của Không mất tính tổng quát ta giả sử bài toán có vị trí tương đối như hình vẽ. Gọi là trung điểm của , là giao điểm (khác ) của với , là trung điểm của . Vì hai tam giác cân nên dễ thấy: Suy ra, tam giác cân tại và tam giác cân tại . Vậy là trung trực của . +) Chứng minh ,đối xứng với nhau qua Ta có: Vậy hai điểm và đối xứng với nhau qua . b) Chứng minh đối xứng với nhau qua Gọi là đường kính của . Ta có nên mà và vuông góc với nhau suy ra là phân giác góc . Vậy đối xứng với nhau qua . +) Dựa vào tính chất của phép đối xứng trục d ta thấy thẳng hàng khi và chỉ khi thẳng hàng. Ta dùng Melenauyt với tam giác để chứng minh điều này. Ta có điều phải chứng minh. [HỘI CÁC TRƯỜNG THPT CHUYÊN VÙNG DUYÊN HẢI VÀ ĐỒNG BẰNG BẮC BỘ- TRƯỜNG THPT CHUYÊN BIÊN HÒA-2006] Cho tam giác với là trực tâm tam giác, là tâm đường tròn ngoại tiếp và là bán kính đường tròn ngoại tiếp. Gọi là điểm đối xứng của qua , là điểm đối xứng của qua , là điểm đối xứng của qua . Chứng minh rằng thẳng hàng khi và chỉ khi . Hướng dẫn giải Gọi là trọng tâm tam giác . A',B',C' lần lượt là trung điểm . Gọi là tam giác nhận là trung điểm các cạnh . Do đó là trọng tâm tam giác . Từ cách dựng suy ra lần lượt là đường trung trực của . Do đó là tâm đường tròn ngoại tiếp tam giác IJK có bán kinh 2R. Gọi là hình chiếu vuông góc của lên các đường . Do là trọng tâm h ... trong đường tròn Các trung tuyến kẻ từ lần lượt cắt tại và. Biết , chứng minh rằng . Hướng dẫn giải Gọi G là trọng tâm của tam giác; lần lượt là trung điểm của và. đồng dạng suy ra đồng dạng suy ra Do nên suy ra: (đpcm) Câu SỞ GIÁO DỤC VÀ ĐÀO TẠO LONG AN KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 VÒNG 1 Cho tam giác không vuông nội tiếp trong đường tròn. Các tiếp tuyến của tại cắt nhau tại. Đường thẳng cắt tại. CMR: . Hướng dẫn giải Dựng BH, CK vuông góc AM Ta có: Tương tự: Suy ra: Câu SỞ GD&ĐT LONG AN KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 VÒNG 1 Cho tam giác nội tiếp đường tròn. Đường phân giác trong góc của tam giác cắt tại và cắt đường tròn tại. Gọi lần lượt là hình chiếu vuông góc của lên và. Chứng minh tam giác và tứ giác có diện tích bằng nhau. Hướng dẫn giải Ta có: AL là đường trung trực của đoạn MK Gọi Đặt , Ta có: đồng dạng với (1) Ta có: Tam giác AML vuông tại M (2) Từ (1) và (2) Câu SỞ GIÁO DỤC VÀ ĐÀO TẠO LONG AN KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 VÒNG 1 Cho tam giác có trực tâm. Đường tròn đường kính cắt BO tại M, đường tròn đường kính cắt tại. Chứng minh . Hướng dẫn giải Gọi H, K lần lượt là chân đường cao kẻ từ B, C của tam giác ABC Ta có đồng dạng với (1) Ta có tam giác AMC vuông tại M, (2) Tương tự: (3) Từ (1), (2),(3) Câu Trường THPT chuyên Long An Cho tứ giác có hai đường chéo cắt nhau tại. Gọi lần lượt là trực tâm của các tam giác và. Gọi là trung điểm. Chứng minh: vuông góc với Hướng dẫn giải Câu Cho hình vuông. Trên các cạnh ta lấy theo thứ tự các điểm sao cho. Xác định vị trí của các điểm sao cho tứ giác có chu vi nhỏ nhất. A D B C E K F G H H O Hướng dẫn giải HAE = DEBF = DFCG = DGHD Þ HE = EF = FG = GH Þ EFGH là hình thoi. Þ Þ Þ Þ EFGH là hình vuông Gọi O là giao điểm của AC và EG. Tứ giác AECG có AE = CG, AE //CG nên là hình bình hành suy ra O là trung điểm của AC và EG, do đó O là tâm của cả hai hình vuông ABCD và EFGH. DHOE vuông cân: HE2 = 2OE2 Þ HE = OE Chu vi EFGH = 4HE = 4OE. Do đó chu vi EFGH nhỏ nhất Û OE nhỏ nhất Kẻ OK ^AB Þ OE ≥OK ( OK không đổi ) OE = OK Û E ≡ K Do đó minOE = OK Như vậy, chu vi tứ giác nhỏ nhất khi và chỉ khi là trung điểm của AB,. Câu Trường THPT chuyên Long An Cho tứ giác nội tiếp Gọi thứ tự là trực tâm của các tam giác. Chứng minh rằng: a) đồng qui. b) Tứ giác là tứ giác nội tiếp Hướng dẫn giải a) Gọi a là khoảng cách từ O tới. Từ tính chất (*) suy ra.Tứ giác AH1 H2B có và AH1 // BH2 (cùng vuông góc với CD ) là hình bình hành. Chứng minh tương tự thì cũng là các hình bình hành. Từ đó suy ra BH1, AH2, CH3, DH4 đồng qui tại trung điểm I của mỗi đường. b) Lấy O1 đối xứng với O qua I; suy ra là hình bình hành. Chứng minh tương tự ta có;;. Suy ra nội tiếp đường tròn Câu Cho tam giác có diện tích bằng 1. Gọi là điểm bất kỳ nằm trong mặt phẳng chứa tam giác. Tìm giá trị nhỏ nhất của biểu thức: (với lần lượt là độ dài các đường cao vẽ từ ). III. Bài toán cực trị (Sở GDĐT Nghệ An- thi chọn học sinh giỏi tỉnh 2004-2005) a. Tìm điểm trong tam giác để nhỏ nhất. b. Xét các tứ giác lồi có độ dài đường chéo , cho trước và góc giữa hai đường chéo có độ lớn đã cho. Hãy xác định tứ giác có chu vi nhỏ nhất. (THPT Chuyên Lê Quý Đôn – Tỉnh Lai Châu- Trại hè Hùng Vương lần X) Trong mặt phẳng cho đường tròn tâm bán kính và một điểm nằm trong đường tròn .Trong các tứ giác lồi nôị tiếp đường tròn nói trên sao cho các đường chéo và vuông góc với nhau tại , hãy xác định tứ giác có chu vi lớn nhất và tứ giác có chu vi nhỏ nhất. Tính các chu vi đó theo và . Lời giải Gọi chu vi tứ giác ABCD là .Ta có Theo định lí P tô lê mê thì: Kẻ đường kính BE,ta có Từ hai đẳng thức trên ta có Chú ý rằng: Thay hai đẳng thức trên và từ ta được: Gọi M,N theo thứ tụ là trung điểm của AC,BD thì Ta có: Do đó Đặt ta có: Từ suy ra: đạt giá trị lớn nhất (hay nhỏ nhất) đạt giá trị lớn nhất (hay nhỏ nhất) đạt giá trị lớn nhất (hay nhỏ nhất) đạt giá trị lớn nhất (hay nhỏ nhất). (THPT Chuyên Hà Giang – Olympic Hùng Vương lần X - 2014) Cho tam giác có chu vi . Các đường phân giác trong , , cắt các đoạn thẳng , , tương ứng tại , , . Đường thẳng qua song song với cắt , theo thứ tự , . Đường thẳng qua song song với cắt , theo thứ tự tại , . Đường thẳng qua song song với cắt , Theo thứ tự , . Chứng minh rằng . Đẳng thức xảy ra khi nào? Lời giải Đặt BC = a, AC = b, BA = c, p = a+b +c. Vì A3A4 || BC nên theo định lí Talet ta có: (1) Áp dụng tính chất đường phân giác trong góc C: Tương tự: Sử dụng công thức đường phân giác cho tam giác ABC và tam giác A1B1C1 Do đó:(2) Từ (1) và (2) ta có: Từ đó, theo bất đẳng thức Cauchy cho hai số dương ta nhận được: (3) Hoàn toàn tương tự:(4); (5) Từ (3), (4) và (5) suy ra:AB4+BC4+CA4+BA3+CB3+AC3a +b+c= p(đpcm) Dấu bằng xảy ra khi a = b =c. VI. Các bài toán khác ( THPT Chuyên Chu Văn An – Lạng Sơn - Thi Toán 11) Cho tam giác vuông tại và là tâm đường tròn nội tiếp của nó. Gọi là đường cao từ đỉnh của tam giác và , lần lượt là tâm đường tròn nội tiếp tam giác , tương ứng. Gọi là trung điểm của . Chứng minh là đường thẳng Euler của tam giác . Lời giải Chứng minh: Ta có và. Tương tự ta có . Gọi giao điểm của AI, BI, CI với EF, FA, AE tương ứng là X, Y, Z. Khi đó, I là trực tâm AEF. Ta có , suy ra . Hoàn toàn tương tự, ta có, nên ta có BEFC nội tiếp, nên suy ra. Vì tứ giác EZYF nội tiếp nên . Hơn nữa, gọi M là trung điểm của YZ, theo định lí Thales suy ra I, M, O thẳng hàng. Mặt khác, các tứ giác AYXE, AZXF nội tiếp nên ta có nên M là tâm ngoại tiếp của XYZ, suy ra M là tâm Euler của AEF, suy ra IM là đường thẳng Euler của AEF nghĩa là OI là đường thẳng Euler của tam giác AEF (THPT Chuyên Nguyễn Tất Thành – Yên Bái – Toán 11) Cho tam giác với trọng tâm nội tiếp trong đường tròn tâm bán kính . Các tia , , cắt đường tròn tại , , . Chứng minh rằng . Lời giải Gọi các trung tuyến của là và đặt Xét phương tích của M đối với đường tròn ta có Từ và từ (2) ta có: Mà khi đó ta được Tương tự ta tính được các tỷ số Ta có Do các dây đều không lớn hơn nên thay vào 4 ta có Từ đó ta có: (Sở GDĐT Quảng Ninh – Chuyên Hạ Long – 2013- Toán 11 ) Cho tam giác cân tại . Gọi là trung điểm của . Đường tròn ngoại tiếp tam giác giao với phân giác góc tại nằm trong tam giác . Đường tròn ngoại tiếp tam giác giao với tại , giao với tại . giao với tại . Chứng minh rằng là tâm đường tròn ngoại tiếp tam giác . Lời giải Gọi D’ là trung điểm của AB và M là trung điểm cạnh BC. Ta có D’ nằm trên đường tròn ngoại tiếp êBCD. Do tính đối xứng nên suy ra suy ra suy ra I nằm trên phân giác góc hay BI là tia phân giác góc (1) 1.0 đ Ta có: => suy ra êAFD cân tại D. 1.0 Do IA.IF = IE.IB nên I thuộc trục đẳng phương của đường tròn đường kính AC và đường tròn ngoại tiếp . Từ đó CI đi qua giao điểm thứ hai J của hai đường tròn này. 1,0 Ta có nên Suy ra hay . Từ đó . Ta có (đpcm) 1.0 (THPT Chuyên Lê Hồng Phong Nam Định – Chọn học sinh giỏi mở rộng 2013-2014 – Toán 11) Cho tứ giác nội tiếp đường tròn . Giả sử cắt tại , cắt tại , cắt tại . Đường thẳng cắt tại . Chứng minh là phân giác của góc . Lời giải Trước hết có bổ đề (Định lý Brocard): Cho tứ giác nội tiếp đường tròn có lần lượt là giao điểm của các cặp cạnh đối và Gọi là giao điểm của hai đường chéo. Khi đó, ta có Thật vậy, gọi là giao điểm khác của đường tròn ngoại tiếp tam giác . Trước hết, ta thấy rằng cùng nằm trên trục đẳng phương của nên chúng thẳng hàng. Ta cũng có nên tứ giác nội tiếp. Tương tự thì tứ giác cũng nội tiếp. Suy ra cũng chính là giao điểm thứ hai khác của hai đường tròn nên các điểm cũng thẳng hàng vì cùng nằm trên trục đẳng phương của hai đường tròn này. Mặt khác, cũng bằng cách xét các góc nội tiếp trong các tứ giác nội tiếp, ta có . Hơn nữa, đây là hai góc bù nhau nên mỗi góc bằng hay . Chứng minh tương tự, ta có hay là trực tâm của tam giác và Định lí được chứng minh. Giải bài toán như hình vẽ dưới Theo định lý trên ta có Chứng minh các tứ giác KDCN và MKCB nội tiếp Thật vậy: Theo hệ thức quen thuộc Suy ra , hay tứ giác KDCN nội tiếp Tương tự ta có MKCB nội tiếp Suy ra Suy ra điều phải chứng minh (THPT Chuyên Lê Quý Đôn Điện Biên – Trại hè lần X – Toán 11) Cho tam giác đều nội tiếp đường tròn . là một điểm di động trên đoạn . Đường thẳng đi qua và vuông góc với cắt cung nhỏ tại . Gọi là hình chiếu của trên . a) Các tiếp tuyến của tại và cắt tiếp tuyến tại của lần lượt tại và . , cắt lần lượt tại và . Chứng minh b) Tìm giá trị lớn nhất của chu vi tam giác theo . Lời giải Có tứ giác AOMD nội tiếp (4) sđ;sđ tứ giác AMGO nội tiếp (5) Từ (4), (5) ta có 5 điểm A, D, M, G, O cùng nằm trên một đường tròn và đồng dạng hay OD.GF = OG.DE. Trên đoạn MC lấy điểm A’ sao cho MA’ = MA đều Chu vi tam giác MAB là Đẳng thức xảy ra khi MC là đường kính của (O) => M là điểm chính giữa cung AM => H là trung điểm đoạn AO Vậy giá trị lớn nhất của chu vi tam giác MAB là 2R + AB Gọi I là giao điểm của AO và BC Giá trị lớn nhất của chu vi tam giác MAB là 2R + AB = (Sở SDĐT Hòa Bình – THPT Chuyên Hoàng Văn Thụ - Đề chọn học sinh giỏi Toán 11) Cho tam giác nội tiếp đường tròn tâm . Đường tròn tâm tiếp xúc với hai cạnh , lần lượt tại , và tiếp xúc trong với đường tròn tâm tại điểm . Một đường thẳng song song với tiếp xúc với đường tròn tâm tại điểm nằm trong tam giác . a. Gọi , lần lượt là giao điểm thứ hai của và với . Chứng minh rằng . b. Chứng minh rằng . Lời giải a) Gọi D là giao điểm thức hai của đường thẳng PC với đường tròn tâm I, và M là giao điểm thứ hai của đường tròn tâm O với PQ. Xét phép vị tự V tâm P biến đường tròn tâm I thành đường tròn tâm O, ta có phép vị tự V biến E, Q, F lần lượt thành K, M, L. Theo tính chất của phép vị tự ta có EF song song với KL. Ta có OK là ảnh của IE qua V, dẫn đến mà , suy ra K là điểm chính giữa của cung AC. Chứng minh tương tự ta có L là điểm chính giữa của cung BC, M là điểm chính giữa của cung AB. b) Ta có (tính chất phép vị tự). (góc tạo bởi tiếp tuyến và dây cung chắn hai cung bằng nhau) và DE = QF. Lại có CE = CF theo tính chất của hai tiếp tuyến kẻ từ một điểm. Suy ra , dẫn đến . Từ đó ta có điều phải chứng minh. ( THPT Chuyên Hùng Vương Tỉnh Phú Thọ – Trại hè Hùng Vương lần X) Tam giác vuông có . Gọi là một điểm trên cạnh , là một điểm trên cạnh kéo dài về phía sao cho Gọi là một điểm trên cạnh sao cho , , , nằm trên một đường tròn. là giao điểm thứ hai của với đường tròn ngoại tiếp tam giác . Chứng minh rằng: . Lời giải Xét các tứ giác nội tiếpvà ta có: (cùng chắn các cung tròn) Mặt khác Xét và có: (do ) (do ) Áp dụng định lí Ptolemy cho tứ giác nội tiếp ta có: Từ( 1), (2), (3) suy ra .■ (Trường PT vùng cao Việt Bắc – Trại hè Hùng Vương lần X) Cho tam giác dều cạnh và một đường thẳng tùy ý. Gọi , , lần lượt là hình chiếu của , , trên . Chứng minh rằng . Lời giải Gọi E là giao của BC và , I, J lần lượt là hình chiếu của B, C trên , K là hình chiếu của C trên . Mặt khác, ta có
Tài liệu đính kèm:
 luyen_de_thi_hoc_sinh_gioi_toan_hinh_hoc_lop_10.docx
luyen_de_thi_hoc_sinh_gioi_toan_hinh_hoc_lop_10.docx





