Tài liệu Hình học Lớp 10 - Phương trình đường thẳng - Năm học 2019-2020 - Võ Văn Rõ

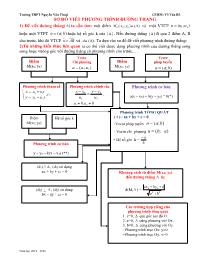
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
SƠ ĐỒ VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG 
1) Để viết đường thẳng   ta cần tìm: một điểm  0 0 0; ( )M x y   và một VTCP 1 2( ; )u u u 
hoặc một VTPT ( ; )n a b hoặc hệ số góc k của   . Nếu đường thẳng   đi qua 2 điểm A, B 
cho trước, khi đó VTCP u AB và ( )A  . Ta dựa vào sơ đồ để viết phương trình đường thẳng: 
2)Từ những kiến thức liên quan ta có thể viết được dạng phương trình của đường thẳng song 
song hoặc vuông góc với đường thẳng có phương trình cho trước, 
Điểm 
M(x0; y0) 
Vectơ 
Chỉ phương 
1 2( ; )u u u 
Vectơ 
pháp tuyến 
 ( ; )n a b 
Điểm 
M(x0; y0) 
Phương trình tham số 
0 1
0 2
,
x x u t
t
y y u t
 

 
Phương trình TỔNG QUÁT 
 ( ) : ax + by + c = 0 
+Vectơ pháp tuyến ( ; )n a b 
+ Vectơ chỉ phương ( ; )u b a  
+ Hệ số góc k = 
a
b

Phương trình cơ bản 
a(x – x0) + b(y – y0) = 0(*) 
Điểm 
M(x0; y0) 
Hệ số góc k 
Phương trình cơ bản 
y – y0 = k(x – x0) (**) 
(d1) //  , (d1) có dạng 
ax + by + c1 = 0 
(d2)   , (d2) có dạng 
bx – ay + c2 = 0 
Khoảng cách từ điểm M(x0; y0) 
đến đường thẳng  là: 
d(M, ) = 
0 0
2 2
ax yb c
a b
 

Các trường hợp riêng của 
phương trình tổng quát 
1. c=0,  qua gốc tọa độ O. 
2. a=0,  cùng phương với Ox. 
3. b=0,  cùng phương với Oy. 
 +Phương trình trục Ox: y=0 
 +Phương trình trục Oy: x=0 
Phương trình chính tắc 
0 0
1 2
x x y y
u u
 
 , 
1 20, 0u u  
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
Một số dạng toán cơ bản về viết phương trình đường thẳng trong mặt phẳng Oxy 
* DẠNG 1: Viết phương trình đường thẳng   đi qua một điểm và có vectơ chỉ phương 
a) Hướng dấn Cách giải 
Phương trình đường thẳng   đi qua điểm 0 0( ; )M x y và có VTCP ( ; )u a b có dạng : 
- Tham số: 0
0
:
( )
x x at
d
y y bt t R
 

   
- Chính tắc: 
 
0 0 
x x y y
a b
( Nếu a.b ≠ 0) 
- Tổng quát: 
0 0( ) ( ) 0b x x a y y    hoặc 0 0( ) ( ) 0b x x a y y     
Chú ý: Nếu   có VTCP ( ; )u a b thì   có VTPT ( ; )n b a  hoặc ( ; )n b a  
b) Ví dụ: Viết phương trình của đường thẳng   biết nó đi qua  1; 2M  và có VTPT  2; 1u   
Giải: 
(ta có thể chọn một trong ba cách viết phương trình của đường thẳng sau để trả lời câu hỏi bài 
toán đưa ra) 
+ Cách 1. Phương trình tham số của đường thẳng ( ) đi qua điểm M(1;-3) và có vtcp 
 2; 1u   có dạng: 
1 2
3
x t
y t
 

  
 t R  
+ Cách 2. Phương trình chính tắc của   là: 
1 3
2 1
x y 


+ Cách 3. Phương trình tổng quát của   do VTCP  2; 1u   nên có VTPT là  1;2n  
nên ta có phương trình tổng quát của   là: 1.( 1) 2( 3) 0 2 5 0x y x y        
* DẠNG 2 : Viết phương trình đường thẳng đi qua một điểm và có vectơ pháp tuyến 
a) Hướng dấn Cách giải: (Ta lựa chọn một trong ba cách viết PTĐT) 
Phương trình đường thẳng   đi qua một điểm 0 0( ; )M x y và có VTPT ( ; )n A B có dạng: 
- Chính tắc:
 


0 0
x x y y
B A
 hoặc 
 


0 0
x x y y
B A
(Nếu A.B ≠ 0) 
- Tham số: 
0
0
:
( )
x x Bt
d
y y At t R
 

   
 hoặc 0
0 ( )
x x Bt
y y At t R
 

   
- Tổng quát: 0 0( ) ( ) 0 0A x x B y y Ax By C        
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
Chú ý: Nếu d có vtpt ( ; )n A B thì d có vtcp ( ; )u B A  hoặc ( ; )u B A  
 Nếu d có vtpt ( ; )n A B thì d có PTTQ có dạng: 0Ax By m   
b) Ví dụ: 
Viết phương trình của đường thẳng   biết nó đi qua  3;2N và có vtpt  3;7n   
Giải: 
(ta có thể chọn một trong ba cách viết phương trình của đường thẳng để trả lời câu hỏi bài toán 
đưa ra) 
  có vtpt  3;7n      có vtcp là  7;3u  
 
 
 
3;2
:
7;3
qua N
vtcp u

 

 có phương trình tham số là: 
3 7
2 3
x t
y t
 

 
 
 
 
3;2
:
3;7
qua N
vtpt n

 
 
 có PTTQ là: 3( 3) 7( 2) 0 3 7 5 0x y x y          
phương trình chính tắc của   là: 
3 2
7 3
x y 


* DẠNG 3 : Viết phương trình đường thẳng đi qua một điểm và có hệ số góc 
a) Hướng dấn Cách giải: Phương trình đường thẳng đi qua điểm M0(x0;y0)và có hệ số góc k là: 
0 0( )y y k x x   
Chú ý: Nếu d có hệ số góc k thì (d) có dạng: y=k.x + m (k≠0, m R, k R) 
b) Ví dụ: Viết phương trình đường thẳng đi qua điểm M0(-5; -8) và có hệ số góc bằng -3 
Giải: 
phương trình trình đường thẳng đi qua điểm M0(-5; -8) và có hệ số góc bằng -3 có dạng là: 
     8 3( 5) y=-3x-23 y x 
Chú ý: Hoặc ta có thể viết PTĐT này dưới dạng PTTS hoặc PTTQ 
Hướng dấn: Vì   có hệ số góc 3k   nên   có vtcp là  1; 3u   rồi viết PTTS hoặc PTTQ 
* DẠNG 4 : Viết PTĐT ( d) đi qua hai điểm phân biệt A(
1 1;x y ) và B( 2 2;x y ) 
a) Hướng dấn Cách giải: (Ta lựa chọn một trong ba dạng viết PTĐT để trả lời câu hỏi bài toán) 
- Tính toạ độ vecto AB 
- Khi đó AB cũng chính là một vtcp của đường thẳng   đi qua 2 điểm A và B 
- Trở lại bài toán dạng: viết phương trình đường thẳng đi qua một điểm (A hoặc B) có vtcp ( AB ) 
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
Chú ý: Đường thẳng   căt Ox, Oy lần lượt tại các điểm A(a;0), B(0;b) có pt là: 
  1 
x y
a b
  . 0a b  
b) Ví dụ: Viết PTĐT   đi qua hai điểm phân biệt    4;1 , 4;2M N 
Giải 
 Vì   qua điểm    4;1 , 4;2M N nên có vtcp là  0;1MN  
 
 
 
4;1
:
0;1
qua M
vtcp MN

 

 nên có phương trình tham số là: 
4
1
x
y t


 
Chú ý:   qua    4;1 ; 4;2M N nên có vtcp là MN hoặc NM ; khi viết ptts thì   đi qua điểm 
M hoặc điểm N đều được. 
* DẠNG 5 : Viết PTĐT ( d) đi qua một điểm M0(x0;y0) và song song với một đường thẳng (d’) 
cho trước có dạng là: 0Ax By C   
a) Hướng dấn Cách giải: 
Cách 1: 
- Dựa vào giả thuyết để tìm vtcp u (hoặc vtpt n ) của đường thẳng (d) 
- Viết PTĐT (d): Viết PTTS của (d) đi qua điểm M0(x0;y0) và có vectơ chỉ phương u hoặc viết 
PTTQ của (d) đi qua điểm M0(x0;y0) và có vectơ pháp tuyến n 
Cách 2: 
- Vì (d) // (d’) nên (d) có dạng: 0Ax By m   (*) 
- Vì M0(x0;y0) (d) thay toạ độ điểm M vào (*) và tính được m 
- Thay giá trị của m vừa tìm vào (*) ta được phương trình đường thẳng (d) cần tìm 
Chú ý: Hai đường thẳng song song với nhau thì vtcp (vtpt) của đường thẳng này cũng chính là 
vtcp (vtpt) của đường thẳng kia. 
b) Ví dụ: Viết PTĐT ( ∆) đi qua một điểm Q (2;1) và song song với đường thẳng (d’) : 
2 5 0x y   
Giải: 
Cách 1: 
 d có vtpt là  2;1n  
M N 
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
  song song với đường thẳng d có pt: 2 5 0x y   nên   có vtpt là:  2;1n     có vtcp 
là:  1; 2u   
 
 
 
2;1
:
1; 2
qua Q
vtcp u

 
 
 nên có ptts là: 
2
1 2
x t
y t
 

 
Cách 2: 
Vì (∆) // (d) nên (∆) có dạng: 2 0x y m   (*) 
Mặt khác Q (2;1)  (∆) nên 2.2 + 1+m = 0 m= -5 
Vậy PTĐT (∆) cần tìm có dạng là: 2 5 0x y   
Nhận xét: Ta dễ nhận xét cách giải quyết bài toán của cách 2 là khoa học và tốt hơn cách 1. 
* DẠNG 6 : Viết PTĐT ( d) đi qua một điểm M0(x0;y0) và vuông với một đường thẳng ∆ cho 
trước có dạng là: 0Ax By C   
a) Hướng dấn Cách giải: 
Cách 1: 
- Dựa vào giả thuyết để tìm vtcp u (hoặc vtpt n ) của đường thẳng (d) 
- Viết PTĐT (d): Viết PTTS của (d) đi qua điểm M0(x0;y0) và có vectơ chỉ phương u hoặc viết 
PTTQ của (d) đi qua điểm M0(x0;y0) và có vectơ pháp tuyến n 
Cách 2: 
- Vì d   nên phương trình (d) có dạng: 0Bx Ay m   (hoặc 0Bx Ay m    ) (*) 
- Vì M0(x0;y0) (d) thay toạ độ điểm M vào (*) và tính được m 
- Thay giá trị của m vừa tìm vào (*) ta được phương trình đường thẳng (d) cần tìm 
Chú ý 1: Hai đường thẳng vuông góc với nhau thì vtcp (vtpt) của đường thẳng này chính là vtpt 
(vtcp) của đường thẳng kia. 
Chú ý 2: Nếu d vuông với một đường thẳng : y=kx+m thì đường thẳng d có phương trình dạng: 
y=
1
k

 x+n (Vì hai đường thẳng vuông góc có tích hệ số góc bằng -1) 
b) Ví dụ: Viết PTĐT ( d) đi qua một điểm P (-1;1) và vuông góc với đường thẳng (∆) : 
2 3 1 0x y   
Giải: 
Cách 1: 
∆ 
d 
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
   có vtpt là  2; 3n   
 (d) vuông góc với đường thẳng   có pt: 2 3 1 0x y   nên  d có vtcp là:  2; 3u   
 
 
 
1;1
:
2; 3
qua P
d
vtcp u


 
 nên có ptts là: 
1 2
1 3
x t
y t
  

 
Cách 2: 
Vì (d)  (∆) nên (d) có dạng: 3 2 0x y m   (*) 
Mặt khác P (-1;1)  (d) nên 3.(-1) + 2.1+m = 0 m= 1 
Vậy PTĐT (∆) cần tìm có dạng là: 3 2 1 0x y   
Nhận xét: Ta dễ nhận xét cách giải quyết bài toán của cách 2 là khoa học và tốt hơn cách 1. 
* DẠNG 7 : Viết PTĐT ( d) đi qua một điểm M0(x0;y0) và tạo với đường thẳng ∆ một góc  cho 
trước (Bài toán liên quan đến góc) 
a) Hướng dấn Cách giải: 
- Gọi phương trình đường thẳng (d) đi qua M0(x0;y0) và có hệ số góc k có dạng là: 
  
0 0
 ( ) y y k x x  0 0 0kx y y kx    (2) 
-Sau đó áp dụng công thứ tính góc giữa hai đường thẳng d và ∆ từ đó suy ra giá trị k cần tìm 
- Thay giá trị k vừa tìm vào (2) ta được PTĐT (d) 
b) Ví dụ: Cho đường thẳng (∆) : 3x-2y+1=0. Viết PTĐT (d) đi qua điểm M (1;2) và tạo với (∆) 
một góc 450 
Giải: 
PTĐT (d) được viết dưới dạng: y – 2 = k ( x-1)  kx – y +2 – k = 0 
Vì (d) hợp với (∆) một góc 450 
nên:
2
| 3 ( 1).( 2) | 2 | 3 2 | 2 9 12 40
cos 45
22 2 22 4 13.( 1)1. 32 ( 2) 13. 1
k k k k
kk k
     
    
   
1
2
5 24 5 0 5
5
k
k k
k

    
 




Vậy phương trình (d) là: 
1 1
2 0 5 9 0
5 5
x y x y        
 hay 5 2 ( 5) 0 5 7 0x y x y          
d 
∆ 
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
5
5
M2
M1
A
d
* DẠNG 8 :Viết PTĐT (∆) đi qua điểm M0(x0;y0) và cách điểm N( 1 1; )x y một khoảng bằng a. 
(Bài toán liên quan đến khoảng cách) 
a) Hướng dấn Cách giải: 
- Gọi phương trình đường thẳng (∆) đi qua M0(x0;y0) và có hệ số góc k có dạng là: 
  
0 0
 ( ) y y k x x  0 0 0kx y y kx    (2) =>ta cần tính số k? 
-Áp dụng công thức: d(N,∆)=a. Từ đó suy ra giá trị k cần tìm 
- Thay giá trị k vừa tìm vào (2) ta được PTĐT (∆) 
b) Ví dụ: Lập phương trình đường thẳng ∆ đi qua M(2;7) và cách N(1;2) một khoảng bằng 1. 
Giải: 
PTĐT (∆) ®i qua ®iÓm M(2; 7) và có hệ số góc k có dạng là: 
   7 ( 2) y k x  7 2 0kx y k    (2’) 
Vì (∆) cách N(1;2) một khoảng bằng 1 nên: 
Ta có: d(N, ∆) =1 
| .1 2 7 2. | | 5 | 2 2 2
1 1 ( 5) ( 1)
2 2
1 1
122 2
10 25 1
5
k k k
k k
k k
k k k k
    
        
 
      
Vậy phương trình (∆) là: 
12 12
7 2. 0 12 5 11 0
5 5
x y x y        
 Qua dạng này họ ... i xứng với đường thẳng  d qua điểm I. 
Giải 
Dễ thấy    0;1A d ; gọi A là điểm đối xứng với A qua I suy ra  2;1A 
(với I là trung điểm của AA’) 
A’ d1 
A 
d 
I  
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
Vì    1 / /d d nên phương trình ( 1d ) có dạng: 2 0x y c   
 1d qua  2;1A nên: 2 2.1 0 0c c     
* DẠNG 10: Tìm hình chiếu của điểm A xuống đường thẳng ∆ (Tìm tọa độ điểm  H   sao 
cho MH ngắn nhất); tìm điểm đối xứng của điểm A qua đường thẳng ∆ 
a) Hướng dấn Cách giải: 
Cách 1: 
Bước 1: Viết pt đường thẳng d đi qua A và d vuông góc với ∆ 
Bước 2: Gọi H là hình chiếu của A trên ∆. Khi đó H d  
Bước 3: A là điểm đối xứng của A qua đường thẳng ∆ khi và chỉ khi H là trung điểm của AA 
Cách 2: Nếu pt ∆ cho dưới dạng tham số: 0 1
0 2
x x u t
y y u t
 

 
Bước 1: Gọi H là hình chiếu của A trên ∆ thì  H    0 1 0 2;H x u t y u t    tọa độ AH 
Bước 2: Do AH   nên AH u  . 0AH u  t  tọa độ H 
Bước 3: A là điểm đối xứng của điểm A qua đường thẳng ∆ khi và chỉ khi H là trung điểm của 
AA 
Cách 3: Nếu pt ∆ cho dưới dạng tổng quát: 0ax by c   
Gọi  ;H HH x y là hình chiếu của điểm A trên ∆ 
Khi đó 
H
AH


 
0H HH ax by c    (1) 
 ;H A H AAH AH x x y y     cùng phương với  ;n a b 
Do đó:     0H A H Ab x x a y y    (2) 
Giải (1) và (2) ta được tọa độ điểm H 
b) Ví dụ: Cho đường thẳng   : 2 4 0x y    và điểm  4;1A 
a) Tìm tọa độ hình chiếu của A trên   
b) Tìm điểm A là điểm đối xứng của A qua   
Giải 
a) + Gọi H là hình chiếu của A trên   
Đường thẳng AH    pt AH có dạng: 2 0x y c   
AH đi qua A nên: 2.4 1 0 9c c      
Vậy phương trình AH là: 2 9 0x y   
+  H AH   
Tọa độ H là nghiệm hệ: 
14
2 9 0 5
2 4 0 17
5
x
x y
x y
y

   
 
    

14 17
;
5 5
H
 
  
 
b) A là điểm đối xứng của A qua   H là trung điểm của AA 
A’ 
∆ 
A 
H 
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
8
8 2952
;
29 5 5
52
A A
AH
A A
AH
x x
xx
A
y y
yy




  
    
     
    
 
Chú thích: Dạng 10 không phải bài toán viết phương trình đường thẳng nhưng giúp ta giải quyết 
bài toán ở dạng 11. 
* DẠNG 11: Viết PTĐT (d’) đối xứng với đường thẳng  d qua đường thẳng ( ) 
a) Hướng dấn Cách giải: 
Để giải các bài toán này, trước tiên ta nên xét chúng cắt nhau hay song song. 
  Nếu (d)// ( ) 
- Bước 1: Lấy A(d). Xác định điểm A’ đối xứng với điểm A qua ( ) 
- Bước 2: Viết phương trình đường thẳng (d’) qua A’ và song song với (d) 
  Nếu (d) cắt ( ) tại điểm I 
- Bước 1: Lấy A(d) (A≠I). Xác định điểm A’ đối xứng với điểm A qua ( ) 
- Bước 2: Viết phương trình đường thẳng (d’) qua A’ và I. 
b) Ví dụ: Cho hai đường thẳng (d1) : -1 0x y  và 2( ) : 3 3 0d x y   . Lập phương trình 
đường thẳng  3d đối xứng với (d1) qua (d2). 
Giải 
 Xét (d1) và (d2) , Ta có: 
1 1
1 3


. Vậy (
1d ) cắt ( 2d ) tại điểm I 
 Tọa độ điểm I là nghiệm của hệ 
-1 0
3 3 0
x y
x y
 
  



=> I(0;1) 
Lấy A(1;0) (d1) 
Gọi A’ là điểm đối xứng với A qua (d2) nên A’
1 12
;
5 5
 
 
 
 (tìm tọa độ A’ dựa vào dạng 10) 
Vậy phương trình của  3d là phương trình của đường thẳng đi qua hai điểm I và A’ 
  3d : 7 1 0x y   
* DẠNG 12 : Viết phương trình đường phân giác của góc tạo bởi hai đường thẳng (d1) và (d2). 
Với: (d1) : 1 1 1 0A x B y C   và (d2): 2 2 2 0A x B y C   
a) Hướng dấn Cách giải: 
- Tính tích vô hướng của 2 vecto 1 2,n n lần lượt là vtpt của (d1) , (d2) 
- Phương trình đường phân giác của góc tạo bởi (d1) và (d2): 
   

 2 2 2 2
' '
' '
Ax By C A x B y C
A B A B
-Khi đó: tồn tại 2 đường phân giác vuông góc với nhau của góc tạo bởi (d1) vµ (d2): 
 
        
   
 
    
1 2
2 2 2 2 2 2 2 2
' ' ' '
 ( ): ( ): 
' ' ' '
Ax By C A x B y C Ax By C A x B y C
A B A B A B A B
- Tuỳ vào yêu cầu đề toán mà ta phải biết cách phân biệt đường phân giác góc nhọn, góc tù; 
đường phân giác góc trong, ngoài của góc tam giác để suy ra PTĐT mà ta cần tìm. 
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
Dựa vào bảng sau: 
1 2.n n 
Phương trình phân giác 
góc nhọn 
Phương trình phân giác góc tù 
- (∆1) 
2
( ) 
+ 
2
( ) (∆1) 
Chú ý 1: Vị trí tương đối của hai điểm đối với đường thẳng: 
 Cho đường thẳng : 0 d ax by c   và 2 điểm ( ; ), ( ; ) A A B BA x y B x y 
Ký hiệu: , A A A B B BT ax by c T ax by c      
Lúc đó: 
 TH 1:    . . 0A B A A B BT T ax by c ax by c      
thì A, B cùng phía đối với đường thẳng d . 
TH 2:    . . 0A B A A B BT T ax by c ax by c      
thì A, B khác phía đối với đường thẳng d . 
Chú ý 2: + Nếu phương trình đường thẳng cho dưới dạng tham số, chính tắc thì ta trước hết phải 
đưa về dạng tổng quát 
+ Khoảng cách giữa hai đường thẳng song song bằng khoảng cách từ một điểm tùy ý trên đường 
thẳng này đến đường thẳng kia. 
b) Ví dụ: 
1) Cho : 3 6 0; :3 2 0d x y d x y      
a) Chứng minh d cắt d’ 
b) Lập phương trình hai đường phân giác của các góc tạo bởi d và d’ 
Giải 
a) Vì: 
1 3
3 1
 nên d cắt d’ 
b) Phương trình hai đường phân giác của các góc tạo bởi d và d’ là: 
 
3 6 3 23 6 3 2
3 6 3 210 10
x y x yx y x y
x y x y
       
         
4 0
1 0
x y
x y
  
    
2) Cho 2 đường thẳng (d1):3x+4y-1=0 và (d2): 4x+3y+5 = 0 . Viết phương trình đường phân giác 
góc nhọn tạo bởi (d1) và (d2) 
Giải: 
(d1) có vtpt là  1 3;4n  
(d2) có vtpt là  2 4;3n  
Ta có: 1 2.n n =3.4+4.3=24 >0 
Ta có phương trình :
   
      
 2 2 2 2
3 4 1 4 3 5
 3 4 1 4 3 5 
3 4 4 3
x y x y
x y x y 
Vì 1 2.n n >0 nên phương trình đường phân giác góc nhọn cần tìm là: 
          3 4 1 ( 4 3 5) 7 7 4 0x y x y x y 
d
A
B
Khác phía 
Cùng phía 
d
B
A
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
2.2 Ứng dụng viết phương trình đường thẳng vào bài toán viết phương trình của các loại 
đường thẳng trong tam giác. 
Lưu ý: ta dựa vào kiến thức về cách viết PTĐT của mục 2.1 để hình thành nên kĩ năng viết 
phương trình của các loại đường trong tam giác 
* DẠNG 13 : Viết phương trình đường trung tuyến, đường cao, trung trực, phân giác và cạnh 
của tam giác 
a) Hướng dấn Cách giải: Dựa vào bảng sau để hinh thành nên cách viết PTĐT cần tìm 
Bài toán 
viết PT 
Hình Phương trình tham số Phương trình tổng quát 
Cạnh AB 
tam giác 
0 0( ; )
:
qua A x y
AB
u AB







 nABu
yxAqua
AB 
);(
:
00
Trung 
tuyến AM 




 AMu
yxAqua
AM 
);(
:
00




 nAMu
yxAqua
AM 
);(
:
00
Đường cao 
AH 
B 




 uBCn
yxAqua
AH 
);(
:
00




 BCn
yxAqua
AH 
);(
:
00
Đường 
trung trực 
 











 

uBCn
yyxx
Iqua cBcB

2
;
2: 











 

BCn
yyxx
Iqua cBcB

2
;
2:
Đường 
phân giác Dựa vào dạng 12 trong phần 2.1 để làm 
b) Ví dụ: 
1) Cho tam giác ABC với      4;5 ; 6; 1 ; 1;1A B C  . Viết phương trình tổng quát của cạnh AB, 
đường trung tuyến AM, đường cao AH của tam giác ABC; đường trung trực của cạnh AB. 
Giải 
Phương trình cạnh AB: 
Đường thẳng AB đi qua    4;5 ; 6; 1A B   nên có vtcp là  10; 6AB     đường thẳng AB có 
vtpt là:  6; 10n   
Phương trình tổng quát của AB là:    6 4 10 5 0 6 10 26 0x y x y        
Phương trình đường trung tuyến AM: 
M là trung điểm của BC nên 
5
;0
2
M
 
 
 
Đường trung tuyến AM đi qua  
5
4;5 ; ;0
2
A M
 
 
 
 nên AM có vtcp là 
13
; 5
2
AM
 
   
 
AM có 
vtpt là 
13
5;
2
n
 
  
 
Phương trình tổng quát của đường trung tuyến AM là: 
B 
C 
C B 
M 
A 
C 
H 
A 
B 
C 
I 

A 
A 
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
   
13
5 4 5 0 10 13 25 0
2
x y x y        
Phương trình đường cao AH: 
Đường cao AH đi qua  4;5A và có vtpt  7;2BC  
Phương trình tổng quát của đường cao AH là:    7 4 2 5 0 7 2 38 0x y x y        
Phương trình đường trung trực của AB: 
Gọi K là trung điểm của AB nên  1;2K  
Gọi   là đường trung trực của AB    đi qua điểm  1;2K  và có vtpt  10; 6AB    
Phương trình tổng quát của   là:    10 1 6 2 0 10 6 2 0 5 3 1 0x y x y x y              
2) Lập phương trình đường phân giác trong của góc A của ABC biết      2;0 ; 4;1 ; 1;2A B C 
Giải 
+ Phương trình cạnh AB: 2 2 0x y   
+ Phương trình cạnh AC: 2 4 0x y   
+ Phương trình hai đường phân giác của góc A: 
 
 
3 2 02 2 2 4
3 6 05 5
x y dx y x y
x y d
     
   
  
+ Xét đường phân giác   : 3 2 0d x y   
Thế tọa độ điểm B vào vế trái của d : 1 4 3.1 2 5 0t      
Thế tạo độ điểm C vào vế trái của d : 2 1 3.2 2 5 0t      
Vì 1 2. 0t t  nên B và C nằm cùng phía đối với d d là đường phân giác ngoài 
Vậy đường phân giác trong của góc A là: :3 6 0d x y    
Bài tập 1*: Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có diện tích bằng 
3
2
, 
A(2;–3), B(3;–2). Tìm toạ độ điểm C, biết điểm C nằm trên đường thẳng 
d: 3x – y – 4 = 0. 
Hướng dẫn 
1) PTTS của d: 
x t
y t4 3
 

  
. Giả sử C(t; –4 + 3t)  d. 
  S AB AC A AB AC AB AC
2
2 21 1
. .sin . .
2 2
   = 
3
2
  t t
2
4 4 1 3    
t
t
2
1
  
 
  C(–2; –10) hoặc C(1;–1). 
Bài tập 2*:Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có điểm M(–1; 1) là trung 
điểm của cạnh BC, hai cạnh AB, AC lần lượt nằm trên hai đường thẳng 
d1: x y 2 0   và d2: x y2 6 3 0   . Tìm toạ độ các đỉnh A, B, C. 
Trường THPT Nguyễn Văn Thoại GVBM: Võ Văn Rõ 
Năm học 2019 - 2020 
Hướng dẫn 
Toạ độ điểm A là nghiệm của hệ: 
x y
x y
2 0
2 6 3 0
   

  
  A
15 7
;
4 4
 
 
 
. 
 Giả sử: B b b( ;2 )  d1, 
c
C c
3 2
;
6
  
 
 
 d2. 
 M(–1; 1) là trung điểm của BC  
b c
c
b
1
2
3 2
2
6
1
2
 
 

 
 


  
b
c
1
4
9
4



  

  B
1 7
;
4 4
 
 
 
, C
9 1
;
4 4
 
 
 
. 
Bài tập 11*:Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác có phương trình hai cạnh là AB: 
5x – 2y + 6 = 0 và AC: 4x + 7y – 21 = 0. 
Viết phương trình cạnh thứ ba của tam giác đó, biết rằng trực tâm của nó trùng với gốc tọa độ O. 
Hướng dẫn 
Giả sử AB: 5x – 2y + 6 = 0; AC: 4x + 7y – 21 = 0  A(0;3) 
 Phương trình đường cao BO: 7x – 4y = 0  B(–4; –7) 
 A nằm trên Oy, vậy đường cao AO nằm trên trục Oy  BC: y + 7 = 0