Giáo án Đại số 10 CB tiết 13, 14: Hàm số bậc hai

Ngày soạn : 
Ngày dạy :
Tiết PPCT : 13 & 14.
	§3. HÀM SỐ BẬC HAI.
I / MỤC TIÊU HỌC TẬP:
Học sinh biết lập bảng biến thiên và vẽ đồ thị hàm số bậc hai.
II / CHUẨN BỊ:
Sách GK, sách GV, tài liệu, thước kẻ, compa, máy tính bỏ túi, thước vẽ parabol  Phiếu học tập.
III / PHƯƠNG PHÁP, PHƯƠNG TIỆN DẠY HỌC:
Phương pháp vấn đáp gợi mở, vấn đáp đan xen hoạt động nhóm thông qua các hoạt động điều khiển tư duy.
IV / TIẾN TRÌNH BÀI HỌC:
	TIẾT 13.
Hoạt động của giáo viên
Hoạt động của học sinh
Kiểm tra bài cũ :
Đồ thị của hàm số y = ax + b, y = {x{. Bài tập 1 trang 41.
I/ ĐỒ THỊ CỦA HÀM SỐ BẬC HAI.
Hàm số bậc hai y = ax2 + bx + c (a¹0). 
Hoạt động 1 : Đồ thị hàm số y = ax2 (a¹0) là parabol đã học ở lớp 9 (phân biệt hai trường hợp a > 0, a < 0).
Liên hệ đồ thị hàm số y = ax2 (a¹0) với đồ thị hàm bậc hai y = ax2 + bx + c.
Cách vẽ parabol (P) : y = ax2 + bx + c (a¹0).
Tọa độ đỉnh.
Trục đối xứng.
Tìm một số điểm thuộc (P).
Vẽ (P) (chú ý a > 0, a < 0).
Thí dụ.
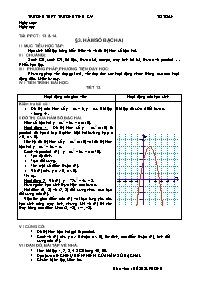
Hoạt động 2 : Vẽ (P) : y = -2x2 + 4x + 3.
Hướng dẫn học sinh thực hiện các bước.
Hai điểm (0; 3) và (2; 3) đối xứng nhau qua trục đối xứng của (P).
Việc tìm giao điểm của (P) với trục tung yêu cầu học sinh dùng máy tính, nhưng khi vẽ (P) thì nên thay bằng các điểm khác (3; -3), (-1; -3).
Bài tập đã sửa ở tiết trước.
V / CỦNG CỐ:
Đồ thị hàm bậc hai gọi là parabol.
Cách vẽ (P): chú ý a > 0 (hoặc a < 0), tìm đỉnh, các điểm thuộc (P), tính đối xứng của (P).
VI / DẶN DÒ, BÀI TẬP VỀ NHÀ:
Làm bài tập 1, 2, 3, 4 SGK trang 49, 50.
Đọc trước II/ CHIỀU BIẾN THIÊN CỦA HÀM SỐ BẬC HAI.
Chuẩn bị ôn tập, kiểm tra.
	TIẾT 14.
Hoạt động của giáo viên
Hoạt động của học sinh
Kiểm tra bài cũ :
Cách vẽ parabol (P) : y = ax2 + bx + c (a¹0)
Bài tập 1 trang 49.
II/ CHIỀU BIẾN THIÊN CỦA HÀM SỐ BẬC HAI.
Liên hệ đồ thị hàm số với bảng biến thiên và ngược lại. Hướng dẫn học sinh nhìn vào bảng biến thiên (cuối trang 45) để liên hệ tính đồng biến, nghịch biến và dạng đồ thị.
Bài tập 2.
y = 3x2 - 4x +1.
Liên hệ giữa y = 3x2 với y = 3x2 - 4x +1 ( a > 0).
Hoành độ đỉnh x = 2/3.
Yêu cầu học sinh dựa vào công thức của hàm số để tính tung độ đỉnh. Hướng dẫn học sinh sử dụng máy tính.
Hướng dẫn học sinh lập bảng biến thiên
Liên hệ bảng biến thiên với hình dạng đồ thị.
Vẽ đồ thị.
Bài tập 3.
Phương pháp giải tương tự bài tập 2 trang 42 đã sửa.
Giải hệ hai phương trình hai ẩn để tìm a, b.
Hướng dẫn học sinh phương pháp giải kết hợp với sử dụng máy tính.
Củng cố : điểm thuộc đường (đường đi qua điểm); tọa độ đỉnh; trục đối xứng.
Bài tập 4.
Phương pháp giải tương tự bài tập 3.
Giải hệ ba phương trình ba ẩn để tìm a, b.
Tọa độ đỉnh.
Trục đối xứng.
Tìm một số điểm thuộc (P).
Vẽ (P)
 x -¥ 2/3 +¥
 +¥ +¥
 y -1/3 
 ó 
V / CỦNG CỐ:
Cách vẽ (P): chú ý a > 0 (hoặc a < 0), tìm đỉnh, các điểm thuộc (P).
(P) đối xứng qua đường thẳng x = -b/2a.
VI / DẶN DÒ, BÀI TẬP VỀ NHÀ:
Chuẩn bị ôn tập, kiểm tra.
Bài tập ôn chương II trang 50, 51.
2a) y = 3x2 - 4x + 1.
2b) y = - 3x2 + 2x - 1.
 x -¥ 2/3 +¥
 +¥ +¥
 y -1/3 
 x -¥ 1/3 +¥
 -2/3 
 y -¥ -¥
2c) y = 4x2 - 4x + 1.
2d) y = - x2 + 4x - 4.
 x -¥ 1/2 +¥
 +¥ +¥
 y 0
 x -¥ 2 +¥
 0 
 y -¥ -¥
2e) y = 2x2 + x + 1.
2f) y = - x2 + x - 1.
 x -¥ -1/4 +¥
 +¥ +¥
 y 7/8 
 x -¥ 1/2 +¥
 -3/4 
 y -¥ -¥