Giáo án Hình cơ bản 10 - Chương III - Tiết 40, 41, 42, 43, 44: Ba đường cônic
A.Elip:
I.Định nghĩa:
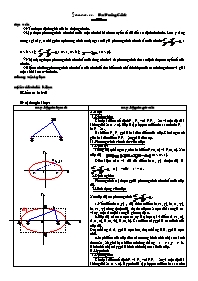
Cho hai điểm cố định F1, F2, với F1F2 = 2c và một độ dài không đổi 2a (a > c). Elip là tập hợp các điểm M sao cho MF1 + MF2 = 2a.
Hai điểm F1, F2 gọi là hai tiêu điểm của elip. Khoảng cách giữa hai tiêu điểm F1F2 = 2c gọi là tiêu cự.
Bạn đang xem tài liệu "Giáo án Hình cơ bản 10 - Chương III - Tiết 40, 41, 42, 43, 44: Ba đường cônic", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
§40-41-42-43-44: Ba Ñöôøng Coânic & I.Muïc tieâu: Nắm được định nghĩa của ba đường cônic. Lập được phương trình chính tắc của một cônic khi cho các yếu tố đủ để xác định cônic đó. Lưu ý rằng trong sgk này, ta chỉ gọi các phương trình có dạng sau đây là phương trình chính tắc của cônic:, ( 0 < b < a ); , ( 0 < a, 0 < b ); , ( 0 < p ). Nhận dạng được phương trình chính tắc của từng cônic và từ phương trình đó xác định được các yếu tố của cônic. Biết cách dùng phương trình chính tắc của cônic để tìm hiểu tính chất hình học của các đường côníc và giải một số bài toán về cônic. II.Phöông tieän daïy hoïc: III.Tieán trình toå chöùc baøi hoïc: ¬Kieåm tra baøi cuõ: x y 0 M (E) Noäi dung baøi hoïc: Hoaït ñoäng cuûa hoïc sinh Hoaït ñoäng cuûa giaùo vieân x y 0 M(x,y) F1 F2 x y 0 F1 F2 M A1 A2 (H) x y 0 F (D) M (P) // = A.Elip: I.Định nghĩa: Cho hai điểm cố định F1, F2, với F1F2 = 2c và một độ dài không đổi 2a (a > c). Elip là tập hợp các điểm M sao cho MF1 + MF2 = 2a. Hai điểm F1, F2 gọi là hai tiêu điểm của elip. Khoảng cách giữa hai tiêu điểm F1F2 = 2c gọi là tiêu cự. II.Phương trình chính tắc của elip: 1.Định lý: Trong mặt phẳng 0xy, cho hai điểm F1(-c, 0) và F2(c, 0). Xét elip (E) = , (0 < c < a). Điều kiện cần và đủ để điểm M(x, y) thuộc (E) là (1) với b2 = a2 – c2. 2.Định nghĩa: Phương trình (1) được gọi là phương trình chính tắc của elip (E). 3.Hình dạng của elip: Xét elip (E) có phương trình . a.Nếu điểm M(x, y) Î (E) thì các điểm M1(-x, y), M2(x, -y), M3(-x, -y) cũng thuộc (E), do đó elip có 2 trục đối xứng là 0x và 0y, một tâm đối xứng là gốc toạ độ 0. b.Elip (E) cắt các trục 0x, 0y lần lượt tại 4 điểm A1(-a, 0), A2(a, 0), B1(0, -b), B2(0, b). Các điểm này gọi là các đỉnh của elip (E). Đoạn thẳng A1A2 gọi là trục lớn, đoạn thẳng B1B2 gọi là trục nhỏ. c.Mọi điểm của elip đều nằm trong hình chữ nhật có kích thước 2a, 2b, giới hạn bởi các đường thẳng x = ± a, y = ± b. Hình chữ nhật này gọi là hình chữ nhật cơ sở của elip. B.Hypebol: I.Định nghĩa: Cho hai điểm cố định F1 và F2, với F1F2 = 2c và một độ dài không đổi 2a (a < c). Hypebol là tập hợp các điểm M sao cho . Hai điểm F1, F2 gọi là hai tiêu điểm của hypebol, khoảng cách giữa hai tiêu điểm F1F2 = 2c gọi là tiêu cự. II.Phương trình chính tắc của hypebol: 1.Định lý: Trong mặt phẳng 0xy, cho hai điểm F1(-c, 0) và F2(c, 0). Xét hypebol (H) : (0 < a < c). Điều kiện cần và đủ để điểm MÎ (H) là: (2) với b2 = c2 – a2. 2.Định nghĩa: Phương trình (2) được gọi là phương trình chính tắc của hypebol (H) 3.Hình dạng của hypebol: Xét hypebol (H) có phương trình . a.Hypebol (H) có hai trục đối xứng là 0x và 0y, một tâm đối xứng là gốc toạ độ 0. b.Hypebol (H) cắt trục hoành tại 2 điểm A1(-a, 0), A2(a, 0) gọi là 2 đỉnh của (H). Đoạn thẳng A1A2 gọi là trục thực; (H) không cắt trục tung 0y, đoạn thẳng B1B2 = 2b gọi là trục ảo với B1(0, -b) và B2(0, b). c.Hypebol (H) gồm hai nhánh: nhánh phải gồm những điểm có hoành độ x ³ a và nhánh trái gồm những điểm có hoành độ x £ -a. d.Hypebol (H) có 2 đường tiệm cận có phương trình . III.Parabol: 1.Định nghĩa: Cho điểm F và đường thẳng (D) không chứa F cố định. Parabol là tập hợp các điểm M sao cho khoảng cách từ M đến F luôn bằng khoảng cách từ M đến đường thẳng (D). Điểm F được gọi là tiêu điểm của parabol và đường thẳng (D) gọi là đường chuẩn. 2.Phương trình chính tắc của parabol: a.Định lý: Trong mặt phẳng 0xy, cho parabol (P) có tiêu điểm F và có đường chuẩn là (D): x = (p > 0). Điều kiện cần và đủ để điểm M(x, y) thuộc (P) là y2 = 2px (3). b.Định nghĩa: Phương trình (3) được gọi là phương trình chính tắc của parabol (P). 3.Hình dạng của parabol: Xét parabol (P) có phương trình y2 = 2px. a.Nếu điểm M(x, y) thuộc (P) thì điểm M1(x, -y) cũng thuộc (P) do đó (P) có trục đối xứng là 0x. (P) cắt trục 0x tại gốc toạ độ 0, đây là đỉnh của parabol. b.Ngoài dạng chính tắc parabol còn có các dạng sau: y2 = -2px; x2 = 2py; x2 = -2py. IV.Ba đường cônic: 1.Giao tuyến của một mặt phẳng với một mặt tròn xoay: Nếu cắt một mặt nón tròn xoay bởi một mặt phẳng không đi qua đỉnh và không vuông góc với trục của mặt nón thì giao tuyến sẽ là elip , hoặc hypebol, hoặc parabol. Người ta gọi ba đường elip, hypebol, parabol là ba đường cônic. 2.Đường chuẩn cuả ba đường cônic: Cho parabol (P) có tiêu điểm F và đường chuẩn (D).Ta có: M Î (P) Û MF = d[M, (D)] Û = 1. Đối với elip (E) hay hypebol (H), tương ứng với mỗi tiêu điểm F luôn có đường thẳng (D) có tính chất: M Î (E) Û = ( < 1); M Î (H) Û = ( > 1). Đường thẳng (D) này được gọi là đường chuẩn của elip hay hypebol. 3.Tính chất chung của ba đường cônic: Cho điểm F , đường thẳng cố định (D) không đi qua F, cho hằng số dương e. Tập hợp những điểm M luôn thoả mãn = e là một cônic (C). Hằng số e này được gọi là tâm sai của cônic (C). e < 1 : (C) là elip. e > 1 : (C) là hypebol. e = 1 : (C) là parabol. ®Cuõng coá: ¯Baøi taäp veà nhaø:hoïc sinh laøm caùc baøi1,2,3,4 trang 97; 1,2,3,4,5 trang 102; 1,2,3,4,5 trang 105 Sgk.
Tài liệu đính kèm:
 40.doc
40.doc





