Giáo án Toán 10 tăng cường tuần 12

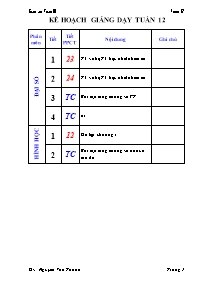
KẾ HOẠCH GIẢNG DẠY TUẦN 12
Phân mơn
Tiết
Tiết PPCT
Nội dung
Ghi chú
ĐẠI SỐ
1
23
PT và hệ PT bậc nhất nhiều ẩn
2
24
PT và hệ PT bậc nhất nhiều ẩn
3
TC
Bài tập tăng cường về PT
4
TC
nt
HÌNH HỌC
1
12
Ơn tập chương 1
2
TC
Bài tập tăng cường về hệ trục tọa độ
Ngày soạn:/ 10 / 2010
Tiết 23 – Đại số
Bàøi 3: PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
BẬC NHẤT NHIỀU ẨN
I. MỤC TIÊU:
	Kiến thức: 	
Nắm vững khái niệm pt bậc nhất hai ẩn, hệ pt bậc nhất hai ẩn và tập nghiệm của chúng.
Hiểu rõ phương pháp cộng đại số và phương pháp thế.
	Kĩ năng: 
Giải được và biểu diễn được tập nghiệm của pt bậc nhất hai ẩn.
Giải thành thạo hệ pt bậc nhất hai ẩn bằng phương pháp cộng và phương pháp thế.
Giải được hệ pt bậc nhất ba ẩn đơn giản.
Giải được một số bài toán thực tế đưa về việc lập và giải hệ pt bậc nhất hai, ba ẩn.
Biết dùng MTBT để giải hệ pt bậc nhất hai, ba ẩn.
	Thái độ: 
Rèn luyện tính cẩn thận, chính xác.
Luyện tư duy linh hoạt thông qua việc biến đổi hệ phương trình.
II. CHUẨN BỊ:
	Giáo viên: Giáo án. Hình vẽ minh hoạ.
	Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về hệ pt bậc nhất hai ẩn.
III. HOẠT ĐỘNG DẠY HỌC:
	1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
	2. Kiểm tra bài cũ: (3')
	H. Nêu dạng của hệ phương trình bậc nhất hai ẩn và phương pháp giải?
	Đ. Phương pháp thế, phương pháp cộng đại số.
	3. Giảng bài mới:
TL
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Ôn tập phương trình bậc nhất hai ẩn
10'
H1. Thế nào là một nghiệm của (1)?
H2. Tìm các nghiệm của pt:
	3x – 2y = 7
(Mỗi nhóm chỉ ra một số nghiệm)
H3. Xác định các điểm (1; –2), (–1; –5), (3; 1),  trên mp Oxy?
Nhận xét?
Đ1. Nghiệm là cặp (x0; y0) thoả ax0 + by0 = c.
Đ2. 
(1; –2), (–1; –5), (3; 1), 
Các điểm nằm trên đường thẳng y = 
1. Phương trình bậc nhất hai ẩn
Dạng: ax + by = c (1)
	trong đó a2 + b2 ≠ 0
Chú ý:
· Þ (1) vô nghiệm
· Þ mọi cặp (x0;y0) đều là nghiệm
· b ≠ 0: (1) Û y = 
Tổng quát:
· Phương trình (1) luôn có vô số nghiệm.
· Biểu diễn hình học tập nghiệm của (1) là một đường thẳng trong mp Oxy.
Hoạt động 2: Ôn tập Hệ hai phương trình bậc nhất hai ẩn
17'
H1. Nhắc lại các cách giải (2)
Áp dụng: Giải hệ:
· HD học sinh nhận xét ý nghĩa hình học của tập nghiệm của (2).
Đ1. Mỗi nhóm giải theo một cách.
· (d1): a1x + b1y = c1
 (d2): a2x + b2y = c2
+ (d1), (d2) cắt nhau Û (2) có 1 nghiệm
+ (d1)//(d2) Û (2) vô nghiệm
+ (d1)º(d2) Û (2) vô số nghiệm
2. Hệ hai phương trình bậc nhất hai ẩn
· Dạng: (2)
· Cặp số (x0; y0) là nghiệm của (2) nếu nó là nghiệm của cả 2 phương trình của (2).
· Giải (2) là tìm tập nghiệm của (2).
Hoạt động 3: Giới thiệu cách giải hệ phương trình bằng định thức
10'
H1. Giải các hệ pt bằng định thức:
a) 
b) 
Đ1. 
a) D = 23, Dx = –23, Dy = 46
Þ Nghiệm (x; y) = (–1; 2)
b) D = 29, Dx = 58, Dy = –87
Þ Nghiệm (x; y) = (2; –3)
· D = 
Dx = , Dy = 
· D ≠ 0: (2) có nghiệm duy nhất 	
· D = 0 và (Dx ≠ 0 hoặc Dy ≠0)
(2) vô nghiệm
· D = Dx = Dy = 0: (2) vô số nghiệm
Hoạt động 4: Củng cố
3'
· Nhắc lại các cách giải hệ phương trình bậc nhất hai ẩn
	4. BÀI TẬP VỀ NHÀ:
1, 2, 3, 4 SGK.
Đọc tiếp bài "Phương trình và hệ phương trình bậc nhất nhiều ẩn"
IV. RÚT KINH NGHIỆM, BỔ SUNG:
Ngày soạn:/ 10 / 2010
Tiết 24– Đại số
Bàøi 3: PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
BẬC NHẤT NHIỀU ẨN (tt)
I. MỤC TIÊU:
	Kiến thức: 	
Nắm vững khái niệm pt bậc nhất hai ẩn, hệ pt bậc nhất hai ẩn và tập nghiệm của chúng.
Hiểu rõ phương pháp cộng đại số và phương pháp thế.
	Kĩ năng: 
Giải được và biểu diễn được tập nghiệm của pt bậc nhất hai ẩn.
Giải thành thạo hệ pt bậc nhất hai ẩn bằng phương pháp cộng và phương pháp thế.
Giải được hệ pt bậc nhất ba ẩn đơn giản.
Giải được một số bài toán thực tế đưa về việc lập và giải hệ pt bậc nhất hai, ba ẩn.
Biết dùng MTBT để giải hệ pt bậc nhất hai, ba ẩn.
	Thái độ: 
Rèn luyện tính cẩn thận, chính xác.
Luyện tư duy linh hoạt thông qua việc biến đổi hệ phương trình.
II. CHUẨN BỊ:
	Giáo viên: Giáo án. Hình vẽ minh hoạ.
	Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về hệ pt bậc nhất hai ẩn.
III. HOẠT ĐỘNG DẠY HỌC:
	1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
	2. Kiểm tra bài cũ: (3')
	H. Giải hệ phương trình sau bằng định thức: 
	Đ. D = 41, Dx = 2, Dy = –48 Þ Nghiệm (x; y) = ()
	3. Giảng bài mới:
TL
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách giải Hệ phương trình bậc nhất 3 ẩn
10'
· GV hướng dẫn tìm nghiệm của hệ phương trình:
–> Hệ phương trình trên có dạng tam giác.
·
(3) Þ z = 
(2) Þ y = 
(1) Þ x = 
II. Hệ phương trình bậc nhất 3 ẩn
· Phương trình bậc nhất 3 ẩn:
	ax + by + cz = d
trong đó a2 + b2 + c2 ≠ 0
· Hệ 3 pt bậc nhất 3 ẩn:
 (4)
Mỗi bộ số (x0; y0; z0) nghiệm đúng cả 3 pt của hệ đgl nghiệm của hệ (4).
· Phương pháp Gauss: Mọi hệ phương trình bậc nhất 3 ẩn đều biến đổi được về dạng tam giác bằng phương pháp khử dần ẩn số.
Hoạt động 2: Luyện tập giải hệ phương trình bậc nhất 3 ẩn
10'
· GV hướng dẫn cách vận dụng phương pháp Gauss.
·
(*) Û 
 Û 
VD1: Giải hệ phương trình:
 (*)
Hoạt động 3: Luyện tập giải toán bằng cách lập hệ phương trình 
10'
H1. Nhắc lại các bước giải toán bằng cách lập phương trình ?
Đ1. 
1) Chọn ẩn, đk của ẩn.
2) Biểu diễn các đại lượng liên quan theo ẩn.
3) Lập pt, hệ pt.
4) Giải pt, hệ pt
5) Đối chiếu đk để chọn nghiệm thích hợp.
· x (đ): giá tiền một quả quýt
 y (đ): giá tiền một quả cam
Þ x = 800, y = 1400
VD2: Hai bạn Vân và Lan đến cửa hàng mua trái cây. Bạn Vân mua 10 quả quýt, 7 quả cam với giá tiền 17800 đ. Bạn Lan mua 12 quả quýt, 6 quả cam hết 18000 đ. Hỏi giá tiền mỗi quả quýt và mỗi quả cam là bao nhiêu?
Hoạt động 4: Hướng dẫn sử dụng MTBT để giải hệ phương trình 
7'
· Hướng dẫn HS sử dụng MTBT để giải hệ pt.
a) 
b) 
VD3: Giải các hệ ph.trình:
a) 
b) 
Hoạt động 5: Củng cố
3'
· Nhấn mạnh cách giải bằng phương pháp Gauss.
	4. BÀI TẬP VỀ NHÀ:
5, 6, 7 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
Ngày soạn:/ 10 / 2010
2 Tiết TC – Đại số
BÀI TẬP TĂNG CƯỜNG VỀ PHƯƠNG TRÌNH
Tuần 12
I- MỤC TIÊU:
- Tăng cường dạng bài tập giải hệ phương trình bậc nhất 2, 3 ẩn. Dạng bài tập “Giải bài tốn bằng cách lập PT, hệ PT, giải hệ ba phương trình bậc nhất 3 ẩn dạng cơ bản. Cách sử dụng máy tính để giải hệ phương trình 2, 3 ẩn.
II- CÁC BÀI TẬP:
Bài 1. Giải các hệ phương trình:
a) 	b) 
	c) 	d) 
Bài 2. Hai bạn Vân và Lan đến cửa hàng mua trái cây. Bạn Vân mua 10 quả quýt, 7 quả cam với giá tiền 17800 đồng. Bạn Lan mua 12 quả quýt, 6 quả cam hết 18000 đồng. Hỏi giá tiền mỗi quả quýt và mỗi quả cam là bao nhiêu.
Bài 3. Giải các hệ PT (sau đĩ kiểm tra kết quả bằng máy tính)
	a) 	b) 
Bài 4 Giải các hệ phương trình sau bằng MTBT (làm trịn kết quả đến chữ số thập phân thứ hai):
	a) 	b) 
	c) 	d) 
BT5. Tìm các giá trị của m để các hệ phương trình sau vơ nghiệm:
	a) 	b) 
Ngày soạn: / 10 / 2010
Tiết 12 – Hình học
ƠN TẬP CHƯƠNG I
I. Mục tiêu
1. Về kiến thức: Củng cố, khắc sâu về
- Véc tơ, tổng và hiệu của 2 véc tơ, phép nhân véc tơ với 1 số
- Quy tắc 3 điểm, quy tắc trừ, quy tắc hbh, t/c của phép cộng, phép nhân véc tơ với 1 số
- Các phép tốn toạ độ của véc tơ và toạ độ của điểm
- Chuyển đổi giữa h2 tổng hợp - toạ độ - véc tơ 
2. Về kĩ năng 
- Thành thạo việc sử dụng quy tắc, t/c vào c/m 1 đt véc tơ 
- Thành thạo các phép tốn về toạ độ của véc tơ, của điểm
- Rèn luyện kĩ năng chuyển đổi giữa h2 tổng hợp - toạ độ - véc tơ
3. Về tư duy 
- Bước đầu hiểu được việc đại số hố hình học
- Hiểu được cách chuyển đổi giữa h2 tổng hợp - toạ độ - véc tơ
4. Về thái độ
- Nghiêm túc, cẩn thận, chính xác
- Bước đầu hiểu được ứng dụng của toạ độ trong tính tốn
II. Chuẩn bị về phương tiện dạy học
1. Thực tiễn
	HS đã được học lý thuyết và biết làm 1 số bài tập cơ bản
2. Phương tiện
	Chuẩn bị các bảng biểu, hình vẽ, đề bài để phát, trình chiếu
III. Phương pháp dạy học
	Gợi mở vấn đáp, chia nhĩm nhỏ học tập
IV. Tiến trình bài học
	A. Các tình huống học tập
	Tình huống 1: Luyện tập về các phép tốn về véc tơ thơng qua các HĐ 1, 2
	HĐ1: HS tiến hành giải bài tập 8 (sgk)
	HĐ2: HS tiến hành giải bài tập 9 (sgk)
	Tình huống 2: Luyện tập về toạ độ của véc tơ và toạ độ của điểm thơng qua các hoạt động 3 5
	HĐ3: Tìm hiểu nhiệm vụ
	HĐ4: HS giải bài tập 11 (sgk)
	HĐ5: HS tiến hành giải bài tập thêm ý a, b, c, d
	Tình huống 3: HĐ6: Chuyển đổi giữa h2 tổng hợp - toạ độ - véc tơ
	 Lập bảng chuyển đổi giữa h2 tổng hợp - toạ độ - véc tơ
	B. Tiến trình bài học 
	1. Kiểm tra bài cũ: Lồng vào các hoạt động trong giờ học
	2. Bài ơn tập
HĐ1: Giải bài tập 8 (sgk)
HĐ của HS
HĐ của GV
- Nhận bài, độc lập tìm lời giải 
- Nhớ lại đ/n tích của véc tơ với 1 số
- Trả lời bài 8 câu a,
- Nhận xét bài làm của 2 HS trên bảng, chỉnh sửa (nếu cĩ)
- Từ đĩ đọc kết quả bài 8/d
- Ghi nhận kq 
- Gọi 2 HS lên bảng làm ý b, c
- Kiểm tra: Tích của véc tơ với 1 số, từ đĩ trả lời câu a, bài 8?
- Kiểm tra bài tập 10 HS
- Theo dõi hoạt động của HS
- Nhận và chính xác hố kết quả của HS
- Sửa chữa kịp thời những sai lầm của HS
- Yêu cầu HS đọc kết quả ý d,
HĐ2: Giải bài tập 9 (sgk)
	CMR: Nếu G và G’ lần lượt là trọng tâm của và thì 
HĐ của HS
HĐ của GV
- Nhớ lại t/c trọng tâm của tam giác
- Nhớ lại p2 c/m 1 đt véc tơ 
- Thực hiện tìm lời giải theo yêu cầu của GV
- Yêu cầu HS nhắc lại t/c trọng tâm của tam giác, quy tắc 3 điểm, p2 c/m 1 đt véc tơ?
- Y/c 1 HS lên bảng làm, số HS ở tại 
- Nhận xét, chỉnh sửa (nếu cĩ)
- Ghi nhận kết quả
- Nêu ĐKCVĐ để và cĩ cùng trọng tâm
- Ghi nhận ĐKCVĐ
lớp c/m bằng cách khác
- Theo dõi hoạt động của HS
- Nhận và chính xác hố kết quả của HS
- Tổng kết: p2 c/m 1 đt véc tơ
- TQ: Đk cần và đủ để và cĩ cùng trọng tâm 
HĐ3: Tìm hiểu nhiệm vụ
Bài tập thêm: Trong mp toạ độ Oxy cho M(1,1); N(7,9); P(5,-3) lần lượt là trung điểm của các cạnh BC, CA, AB của 
	a. Tìm toạ độ của mỗi véc tơ sau: 
	b. Tìm toạ độ điểm E sao cho 
	c. Xác định toạ độ các điểm A, B, C của 
	d. Tính chu vi 
HĐ của HS
HĐ của GV
- Nhận (chép) bài tập 
- Nhớ lại kiến thức liên quan
- Đọc và nêu các thắc mắc về đề bài
- Định hướng cách giải bài tốn
- Giao bài tập cho HS
- Dự kiến nhĩm HS
- Kiểm tra kiến thức:
 Cho . Toạ độ 
HĐ4: Giải bài tập 11 (sgk). Theo nhĩm
HĐ của HS
HĐ của GV
- Nhận bài, tiến hành tìm lời giải theo nhĩm
- Thơng báo kết quả 
- Nhận xét, chỉnh sửa (nếu cĩ)
- Ghi nhận kết quả 
- Giao bài tập cho từng nhĩm?
Nhĩm 1: (a)
Nhĩm 2: (b)
Nhĩm 3: (c)
- Theo dõi hoạt động của HS
- Nhận và chính xác hố kết quả của HS
- Đánh giá mức độ hiểu, vận dụng của các nhĩm
- Sữa chữa những sai lầm của HS
HĐ5: HS tiến hành tìm lời giải bài tập thêm ý a, b, c, d
HĐ của HS
HĐ của GV
- Tìm toạ độ véc tơ 
- Y/c HS trả lời bài tập thêm ý a,
- HS khác nhận xét 
- Tìm toạ độ 
- Tìm toạ độ điểm A, B, C
- Nêu cách khác tìm toạ độ điểm B, C
- Ghi nhận kết quả 
- Ghi nhận cơng thức tính 
- Áp dụng tính AB, BC, CA
 Từ đĩ chu vi 
- Thơng báo kết quả: Toạ độ trọng tâm của , 
- Nêu nhận xét 
- Y/c HS nêu cách giải bài tập ý b,
ĐS: E(-3,-23)
- Y/c Nhĩm 1: Tìm toạ độ điểm A
	 Nhĩm 2: Tìm toạ độ điểm B
 Nhĩm 3: Tìm toạ độ điểm C
- Nhận và chính xác hĩa kết quả của HS 
- Y/c HS nhắc lại cơng thức tính chu vi của ?
- Giới thiệu cơng thức tính độ dài của 1 véc tơ 
- Y/c HS tính: AB? BC? CA?
- Y/c đọc kết quả: Chu vi của ?
- Sửa chữa một số sai lầm của HS 
- Y/c HS đọc kết quả toạ độ trọng tâm của , (cĩ nhận xét )	
HĐ6: Thành lập bảng chuyển đổi giữa h2 tổng hợp - toạ độ - véc tơ
HĐ của HS
HĐ của GV
- Học cách chuyển đổi
- Bắt trước theo mẫu
- Tự hồn thiện bảng
- Hướng dẫn HS cách thành lập bảng chuyển đổi
- GV làm mẫu vài ví dụ, sau đĩ y/c HS cho 1 vài ví dụ
- GV tổng kết thành bảng chuyển đổi
- Cho HS tham khảo bảng chuyển đổi đã chuẩn bị
- GV y/c HS tự hồn thiện bảng
Bảng chuyển đổi giữa hình học tổng hợp - toạ độ - véc tơ
STT
Tổng hợp
Véc tơ
Toạ độ (trên mp)
1
Điểm M là trung điểm của đoạn AB
1. 
2. 
3. 
điểm O
2
Điểm G là trọng tâm của 
1. 
2.
3
Ba điểm A, B, C thẳng hàng
 và 
*) Củng cố:	 Qua bài học các em cần:
	+Thành thạo các phép tốn về véc tơ, các phép tốn về toạ độ của véc tơ và của điểm.
	+ Biết cách chuyển đổi giữa hình học tổng hợp - toạ độ - véc tơ
	3. Bài tập về nhà: Tự hồn thành các bài tập cịn lại
Ngày soạn:/ 10 / 2010
Tiết TC – Hình học
BÀI TẬP TĂNG CƯỜNG VỀ HỆ TRỤC TỌA ĐỘ
TUẦN 12
I- MỤC TIÊU:
- Tăng cường các dạng bài tập tổng hợp về hệ trục tọa độ. Thực hiện dạng bài tập: tính tọa độ vectơ theo tọa độ điểm, các dạng bài tập khác: chứng minh – tìm vectơ cùng phương, chứng minh – tìm hình bình hành .
II- CỦNG CỐ LÝ THUYẾT:
1) Tọa độ vectơ theo tọa độ điểm
Nếu A( xA ; yA) và B( xB ; yB) thì 
2) Cộng, trừ, nhân vectơ 
Cho 
Khi đĩ ta cĩ:
Từ đĩ, hai vectơ và cùng phương nếu cĩ 1 số k thỏa mãn :
 hay 
3) Tọa độ trung điểm, trọng tâm
Nếu I là trung điểm của đoạn thẳng AB thì: 
Nếu G là trọng tâm tam giác ABC thì : 
III- CÁC BÀI TẬP:
DẠNG 1: Hai vectơ cùng phương, bằng nhau:
Bài 1. Trong các cặp vectơ sau, cặp vectơ nào là cùng phương, vì sao?
a) 	b) 
a) 	b) 
Bài 2. Cho ABCD là hình bình hành.
a) A(- 2; 3) ; B(3; 5) ; C(- 1; -3). Tìm D
b) A(1; - 3) ; B(-2 ; -3) ; D(4; -3). Tìm C
c) B(2; - 3) ; C(-2 ; 4) ; D(4; 1). Tìm A
d) A(1; 1) ; C(- 2 ; - 4) ; D(3; 1). Tìm B
Bài 3. Trong các bộ ba điểm sau, bộ ba nào là ba điểm thẳng hàng? Vì sao?
A(- 2; 3) ; B(3; 5) ; C(- 1; -3)
A(2; 1) ; B(-1 ; 2) ; C(0; 3)
A(1; -1) ; B(2 ; 4) ; C(-2; -8)
A(3; 2) ; B(1 ; 2) ; C(-2; -1)
DẠNG 2: Tọa độ vectơ theo tọa độ điểm, tọa độ trung điểm, trọng tâm:
Bài 4. Tìm trung điểm các đoạn thẳng sau:
a) A(1; -1) ; B(2 ; 4)	b) B(1 ; 2) ; C(-2; -1)	c) M(3; 5) ; N(- 1; -3)
Bài 5. Tìm tọa độ trọng tâm các tam giác:
a) A(- 2; 3) ; B(3; 5) ; C(- 1; -3) b) A(1; 1) ; C(- 2 ; - 4) ; D(3; 1)
c) B(2; - 3) ; C(-2 ; 4) ; D(4; 1) d) M(- 2; 3) ; B(3; 5) ; C(- 1; -3)
Bài 6. 
a) Cho M là trung điểm của AB, biết A(1;3) ; M(-2;-1). Tìm tọa độ B
b) Cho N là trung điểm CD, biết D(-5; -3) ; N(-1;3). Tìm tọa độ C
c) Biết G là trọng tâm tam giác ABC, biết A(1;1) ; B(4;-2); G(3;2). Tìm tọa độ C
d) Biết G’ là trọng tâm tam giác HIK, biết G(-1;2) ; H(1;1) ; K(-2;-4). Tìm tọa độ I
Bài 7: Cho A(1;1) ; B(3;2) ; C(-1;-3). Tìm tọa độ I biết:
a) 	b) 
a) 	b) 	
Bài 8. Cho ba điểm A(-1;1), B(1;3), Tìm vị trí M, biết.
M là điểm thuộc đoạn AB sao cho MA = 2MB
M là điểm nằm ngồi đoạn thẳng AB sao cho MA = 3MB
M là điểm thuộc đoạn AB sao cho MA = 3MB
M là điểm nằm ngồi đoạn thẳng AB sao cho MB = 3MA