Đề cương ôn tập về Phương trình đường thẳng
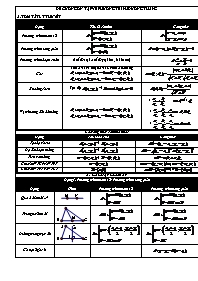
Dạng
Phương trình tham số
Phương trình tổng quát
Phương trình đoạn chắn
Góc
Khoảng cách
Vị trí tương đối 2 đthẳng
Bạn đang xem tài liệu "Đề cương ôn tập về Phương trình đường thẳng", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ĐỀ CƯƠNG ÔN TẬP VỀ PHƯƠNG TRÌNH ĐƯỜNG THẲNG A. TÓM TẮT LÝ THUYẾT Dạng Yếu tố cần tìm Công thức Phương trình tham số Phương trình tổng quát Phương trình đoạn chắn d cắt Ox tại a,cắt Oy tại b (a, b khác 0) Góc Tìm 2 VTPT hoặc 2 VTCP của 2 đ.thẳng Khoảng cách Tọa độ và Vị trí tương đối 2 đthẳng cắt Các công thức cần nhớ khác Dạng Yếu tố đã cho Công thức Tọa độ véctơ và Độ dài đoạn thẳng và Tích vô hướng và Chuyển VTCP về VTPT hoặc Chuyển VTPT về VTCT hoặc CÁC DẠNG CƠ BẢN Dạng 1. Phương trình tham số - Phương trình tổng quát Dạng Hình Phương trình tham số Phương trình tổng quát Qua 2 điểm M, N N M Trung tuyến AM M C B Đường trung trực I C B A Có hệ số góc k Song song với đt d M d’ Vuông góc với đt BÀI TẬP ÁP DỤNG Câu 1. Lập phương trình tham số của đường thẳng d biết d: a) Đi qua và có VTCP b) Đi qua và có VTCP c) Đi qua gốc tọa độ O và có VTCP d) Đi qua và có VTCP e) Đi qua và có VTPT f) Đi qua và có VTPT g) Cho và điểm thỏa . Viết ptts đt đi qua và có VTCP . Câu 2. Viết phương trình tổng quát của đường thẳng trong các trường hợp sau: a) Đi qua và có VTPT b) Đi qua và có VTPT c) Đi qua gốc tọa độ O và có VTPT d) Đi qua và có VTPT e) Đi qua và có VTCP f) Đi qua và có VTCP g) Cho và điểm thỏa . Viết pttq đt đi qua và có VTCP . Câu 3. Viết phương trình tham số của đường thẳng trong các trường hợp sau: a) Đi qua và . b) Đi qua và . c) Đi qua và gốc tọa độ O. d) Đi qua và cắt trục hoành tại 3. e) Đi qua và cắt trục tung tại -2. f) Cắt trục Ox tại và cắt Oy tại -5. Câu 4. Viết phương trình tổng quát của đường thẳng trong các trường hợp sau: a) Đi qua và có hệ số góc . b) Đi qua và có hệ số góc . c) Đi qua và . d) Đi qua và . e) Đi qua và cắt trục tung tại -2. f) Cắt trục Ox tại và cắt Oy tại 3. Câu 5. Cho tam giác có , , . a) Viết phương trình tham số cạnh AB b) Viết phương trình tổng quát cạnh BC. c) Viết phương trình tham số trung tuyến AM. d) Viết phương trình tổng quát đường cao BK. e) Viết pttq đường trung trực của cạnh BC. f) Viết ptts đường trung trực cạnh AC. Câu 6. Cho tam giác có , , . a) Viết phương trình tham số cạnh NP b) Viết phương trình tổng quát cạnh MN. c) Viết phương trình tổng quát trung tuyến MH. d) Viết phương trình tổng quát đường cao PK. e) Viết pttq đường trung trực của cạnh MP. f) Viết ptts đường trung trực cạnh MN. Câu 7. Viết phương trình tham số, phương trình tổng quát của đường thẳng d trong các trường hợp sau: a) Đi qua và song song với b) Đi qua và vuông góc với c) Đi qua và vuông góc với d) Đi qua và song song với . Dạng 2. Vị trí tương đối của hai đường thẳng Cho hai đường thẳng và hệ (*) Vị trí tương đối d1 Hình ảnh Tỉ số Số nghiệm của hệ (*) Cắt nhau d2 Có nghiệm duy nhất Song song d1 d2 Vô nghiệm Cắt nhau d2 Vô số nghiệm BÀI TẬP ÁP DỤNG Câu 8. Xét vị trí tương đối của các cặp đường thẳng và trong các trường hợp sau: a) và b) và c) và d) và e) và f) và g) và h) và Dạng 3. Tính góc giữa hai đường thẳng Hình ảnh Công thức Góc giữa hai đường thẳng và d1 d2 BÀI TẬP ÁP DỤNG Câu 9. Tính góc giữa các cặp đường thẳng sau: a) và b) và c) và d) và e) và f) và trục hoành Câu 10. Cho và . Tìm m để: a) song song với b) vuông góc với Dạng 4. Khoảng cách Yếu tố đã có Công thức Khoảng cách giữa 2 điểm và Khoảng cách từ một điểm đến đường thẳng Điểm và BÀI TẬP ÁP DỤNG Câu 11. Tính khoảng cách từ một điểm đến đường thẳng trong các trường hợp dưới đây: a) và b) và c) và d) và Câu 12. Tìm tọa độ M thỏa: a) M thuộc d: và cách điểm một khoảng bằng 5. b) M nằm trên d: và cách điểm một khoảng bằng . c) M nằm trên trục tung và cách đường thẳng một khoảng bằng 1. d) M nằm trên trục Ox và cách đường thẳng một khoảng bằng 1. ĐỀ KIỂM TRA HÌNH HỌC 10 CHƯƠNG III ĐỀ I Cho tam giác ABC có góc A = 1200 , cạnh AC = 8, cạnh AB = 5. Tính cạnh BC. Tính góc C. Tính bán kính đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác ABC. Câu 1: (3.0 điểm) Trong mặt phẳng Oxy, Cho hai điểm A(1; -3); B(-5;1) và đường thẳng d: . 1.Viết phương trình tham số, phương trình tổng quát của đường thẳng đi qua hai điểm A, B. 2.Gọi K là trung điểm của đoạn thẳng AB. Tính khoảng cách từ K đến đường thẳng d. Câu 2: (3.0 điểm) Trong mặt phẳng Oxy, cho tam giác ABC có A(2;4); B(1;1); C(3;1). 1.Viết phương trình tổng quát của đường trung tuyến AM của tam giác. 2. Viết phương trình của đường cao BH của tam giác. Câu 3: (2.0 điểm) Trong mặt phẳng Oxy, cho đường thẳng: . Tìm một điểm và một vectơ chỉ phương của đường thẳng . Viết phương trình tổng quát của đường thẳng . Câu 4 (2.0 điểm) Viết phương trình của đường thẳng d đi qua A(1; -2) và song song với đường thẳng : ................................................................................................ ĐỀ KIỂM TRA HÌNH HỌC 10 CHƯƠNG II ĐỀ II Câu 1: (3.0 điểm) Trong mặt phẳng Oxy, Cho hai điểm A(1; -2); B(3;2) và đường thẳng d: . Viết phương trình tham số, phương trình tổng quát của đường thẳng m đi qua hai điểm A, B. Gọi K là trung điểm của đoạn thẳng AB. Tính khoảng cách từ K đến đường thẳng d. Câu 2: (3.0 điểm) Trong mặt phẳng Oxy, cho tam giác ABC có A(2;1) ,B(1;-3),C(3;0) Viết phương trình tổng quát của đường trung tuyến AM của tam giác. Viết phương trình của đường cao BH của tam giác. Câu 3: (2.0 điểm) Trong mặt phẳng Oxy, cho đường thẳng: . 1.Tìm một điểm và một vectơ chỉ phương của đường thẳng . 2.Viết phương trình tổng quát của đường thẳng . Câu 4 (2.0 điểm) Viết phương trình của đường thẳng d đi qua P(2; 1) và vuông góc với đường thẳng :
Tài liệu đính kèm:
 phuong trinh duong thang.doc
phuong trinh duong thang.doc





